Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 51

Determine v ( t ) para t > 0 no circuito da Figura 8.98 .

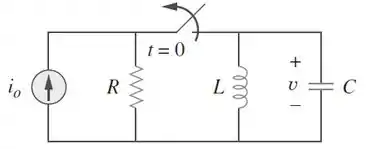
Passo 1

Galerinha, vamos lá. No momento t = 0^- , nós temos o circuito sendo alimentado por uma fonte de corrente, em regime permanente. Sabemos que, sob esse regime, o indutor se comporta como um fio e o capacitor como um circuito aberto. Assim, a corrente i (t) é a corrente da fonte, uma vez que os resistores ficam curto-circuitados:

i (0) = i_0

v (0) = 0

Passo 2

Quando t > 0 , temos um circuito LC paralelo sem fontes ( R = oo ). Logo, a próxima coisa que podemos começar a fazer é analisar os valores de alpha e omega_0 e achar as raízes características:

alpha = (1)/(2 R C) = (1)/(2 (8) (1 0 xx 10^(- 3))) = 0

omega_0 = (1)/(sqrt(L C))

Isso nos leva a ter

s_1,2 = - alpha +- sqrt(alpha^2 - omega_0^2) = +- j omega_0

Portanto, a equação da tensão será da forma:

v (t) = A cos omega_o t + B sin omega_0 t , v (0) = 0

A corrente no capacitor é dada por:

i_C = C (d v)/(d t)

Vamos calcular a derivada da tensão?

(d v)/(d t) = omega_0 B sin omega_0 t = - (i)/(C)

No instante t = 0 , temos:

(d v (0))/(d t) = omega_0 B sin omega_0 t = - (i_0)/(C)

B = (i_0)/(omega_0 C)

Portanto, a nossa tensão será igual a:

v (t) = - (i_0)/(omega_0 C) sin omega_0 t V

Resposta

O valor para v ( t ) é:

v (t) = - (i_0)/(omega_0 C) sin omega_0 t V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule i(t) para t0 no circuito da Figura 8.82.
Determine v(t) para t0 no circuito da Figura 8.83.
Considere o circuito da Figura 8.79. Determine vL(0+) e vc(0+).
Para o circuito da Figura 8.80, determine v(t) para t0.
Determine v(t) para t0 no circuito da Figura 8.81.