Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 1

Calcule v ( t ) para t > 0 se v ( 0^- ) = 10V.

Passo 1

Fala, galerinhaaaa!

Vamos mandar bronca nessa questão de circuito RC. Vamos observar o circuito e pegar as informações que ele nos dá.

Dado o circuito:

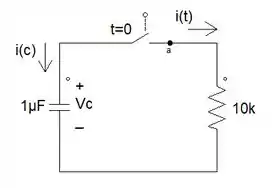
Olhando de cara, já sabemos que esse circuito é um circuito RC sem fonte. Além disso, podemos observar que o capacitor está carregado, então temos que, a tensão v_c (0^-) = 10 V = v_c (0^+) .

Agora, vamos aplicar LKC no nó a, temos que:

i_c + i_r = 0

Sabendo que i_c = C * (d v)/(d t) e i_r = (v)/(R) , vamos substituir:

C * (d v)/(d t) + (v)/(R) = 0

1 µ * (d v)/(d t) + (v)/(10 x 10^3) = 0

Essa equação é uma EDO de 1ª ordem, que se dá pela equação característica:

1 x 10^(- 6) r + (1)/(10 x 10^3) = 0

r = - (1)/(10 x 10^3) x (1)/(1 x 10^(- 6))

r = - (1)/(0,01)

Passo 2

Maravilha! Agora vamos usar o valor do r na equação geral.

v (t) = A e^(r t)

Já sabemos que v (t) = 10 V , r = (1)/(1 x 10^(- 4 )) e t = 0 , vamos descobrir o valor da constante A.

10 = A e^(- (1)/(0,01) x 0)

10 = A e^0

A = 10

Show de bola! Nossa resposta final dessa equação será:

v (t) = 10 e^(- 100 t) V p a r a t > 0 .

Resposta

v (t) = 10 e^(- 100 t) V

Exercícios de Livros Relacionados

Calcule i e v para t0 , se v (0) = - 6 V .
Calcule, para t0 , a corrente que entra para baixo no capacitor, se v ( 0 ) = 0 , e (a) V g = 4 V , (b) V g = 2 e - 2 t V , e (c) V g = 2 C o s 2 t V .
Calcule v para t0 , se o circuito está em regime permanente em t = 0 - .
Calcule v para t0 , se o circuito está em regime permanente em t = 0 - .
Calcule v para t0, se v (0) = 2 V e (a) v_g = 4 V , (b) v_g = 6 e^(- t) V e (c) v_g = 6 e^(- 3 t) V .