Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 11.Problemas - Ex. 49

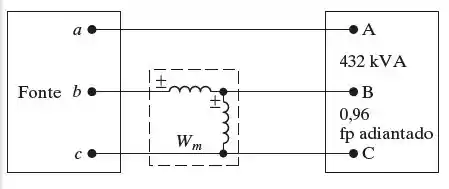
A carga trifásica equilibrada mostrada na Figura P11.49 é alimentada por uma fonte

trifásica, equilibrada, de sequência positiva e ligada em Y. A impedância da linha que liga

a fonte à carga é desprezível. A tensão fase‑neutro da fonte é 7.200 V.

a) Determine a leitura do wattímetro em watts.

b) Explique como conectar um segundo wattímetro ao circuito de modo que os dois wattímetros meçam a potência total.

c) Determine a leitura do segundo wattímetro.

d) Verifique se a soma das leituras dos dois wattímetros é igual à potência média total fornecida à carga.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe circuitos trifásicos equilibrados!

  1. Para essa leitura, inicialmente definimos alguns parâmetros:

    2. I a A * = 144 0,96 - j 0,28 10 3 7200 = 20 / - 16,26 ° A

    V B N = 7200 / - 120 °   V

    V C N = 7200 / - 120 °   V

    Logo:

    V B C = V B N - V C N = 7200 3 / - 90 ° V

    E também:

    I b B = 20 / - 103,74 ° A

    Por fim temos que:

    W m 1 = 7200 3 20 cos ⁡ - 90 ° + 103,74 ° = 242278,14 W

  2. Uma bobina de corrente na linha aA, mede I a A , e uma bobina de tensão em CA, meça V A C .

    3. Passo 2

  3. Para o segundo wattímetro, similar ao primeiro, temos que:

    4. I a A * = 20 / 16 , 7 6 ° A

    Logo:

    V C A = V A N - V C N = 7200 3 / - 3 0 ° V

    Por fim temos que:

    W m 1 = 7200 3 20 cos ⁡ - 3 0 ° - 16,26 ° = 172441,86   W

  4. Para a soma dos wattímetros, temos:

W m 1 + W m 2 = 414,72   k W

Comparando:

P T = 432000 0,96 = 414,72   k W

Resposta

  1. Item a:

    2. W m 1 = 242278,14 W

  2. Uma bobina de corrente na linha aA, mede I a A , e uma bobina de tensão em CA, meça V A C .

  3. Item c:

    4. W m 1 = 172441,86   W

  4. Sim.

Exercícios de Livros Relacionados

Se V a n=220 ∠60 °V no circuito da Figura 12.49, determine, para a carga, as corrente de fase I A B ,I B CeI C A .
Três geradores de 230V formam uma fonte conectada em triângulo que é conectada a uma carga em triângulo equilibrada com Z L = 10 + j 8Ω por fase, conforme mostrado na figura 12.52.Determine o valor de
Para o circuito triângulo-triângulo da Figura 12.50, calcule as correntes de linha e de fase.
Considere a Figura 12.51 e elabore um problema para ajudar outros estudantes a entender melhor os circuitos conectados em triângulo-triângulo equilibrado.
Determine as correntes I a , I b e I c no circuito trifásico da Figura 12.53 a seguir. Adote Z Δ =12–j 5Ω ,Z Y=4+j 6ΩeZ l = 2Ω .