Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 5

Referindo-se ao circuito da Figura 8.66, determine:

(a) i ( 0 + ) e v ( 0 + )

(b) d i ( 0 + ) / d t e d v ( 0 + ) / d t

(c) i ( ∞ ) e v ( ∞ )

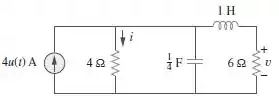
Passo 1

Primeiro vamos analisar o circuito para t = 0 - . Sabemos que, 4u(t) = 0

Por conta disse não há nenhuma fonte de alimentação. Logo,

i L 0 - = 0

v C 0 - = 0

Passo 2

Certo! Agora vamos analisar quando t = 0 + . Então o circuito equivalente é:

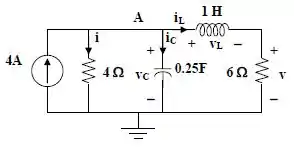
Lembre-se que, no indutor não pode haver mudança abrupta de corrente, e no capacitor uma mudança abrupta de tensão. Então, como o resistor de 4 Ω está em paralelo com o capacitor, temos:

i 0 + = v C 0 + 4

i 0 + = 0   A

Do mesmo modo, o resistor de 6 Ω está em série com o indutor, portanto

v C 0 + = 6 i L 0 +

v C 0 + = 0   V

Passo 3

Para o item b) ainda continuaremos analisando o circuito quando   t = 0 + . Pela lei de Ohm, temos:

i 0 + = v R 0 + R

Derivando,

d i 0 + d t = 1 R d v R 0 + d t

E como,

v C = v R

Então,

d i 0 + d t = 1 R d v C 0 + d t

Lembre-se que,

i c = C d v C 0 + d t

d v C 0 + d t = i C 0 + C

Note que, como o indutor não muda de corrente abruptamente e a tensão no resistor de 4 Ω é 0, então a corrente de 4 A vai toda para o capacitor, logo

i C 0 + = 4   A

Portanto,

d v C d t = 4 0.25 = 16

Logo,

d i 0 + d t = 1 R d v C 0 + d t

d i 0 + d t = 1 4 * 16

d i 0 + d t = 4   A / s

Passo 4

Observe que,

v = 6 i L

Derivando,

d v d t = 6 d i L d t

Aplicando em t= 0 + ,

d v 0 + d t = 6 d i L 0 + d t

Como,

d i L 0 + d t = v L 0 + L

Já sabemos que,

v L 0 + = 0

Logo,

d i L 0 + d t = 0

Então,

d v 0 + d t = 0   V / s

Passo 5

Certo! Estamos quase terminando falta só um item. Esse é só analise de um circuito, no mesmo jeito dos passos anteriores.

Note que, se o tempo tender ao infinito o capacitor é um circuito aberto e o indutor um circuito fechado. Então, por divisor de corrente temos:

i( ∞ ) = 6(4)/(6+4) = 2.4 A

Por lei de Ohm, teremos

v( ∞ ) = 6(4 – 2.4) = 9.6 V

Resposta

  1. i 0 + = 0 A

    2.                                       v 0 + = 0   V

d i ( 0 + ) d t =   4   A / s

d v 0 + d t = 0   V / s

c)

i ∞ = 2.4   A

v ∞ = 9.6   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito da Figura 8.65, determine:(a) v 0 +ei ( 0 + ) (b) d v ( 0 + ) / d ted i ( 0 + ) / d t (c) v ∞ei ( ∞ )
Considere a Figura 8.63 e elabore um problema para ajudar outros estudantes a entenderem melhor como determinar os valores inicial e final.
Para o circuito da Figura abaixo, determine:(a) i L ( 0 + ) , v c ( 0 + ) e v R ( 0 + ) (b) d i L ( 0 + ) / d t , d v C ( 0 + ) / d t e d v R ( 0 + ) / d t (c) i L ( ∞ ) e v C ( ∞ ) e v R ( ∞ ) .
No circuito da Figura 8.67, determine:(a) v R 0 +ev L ( 0 + ) (b) d v R ( 0 + ) / d ted v L ( 0 + ) / d t (c) v R ∞ev L ( ∞ )
A resposta a um degrau de um circuito R L C é descrita por d 2 i d t 2 + 2 d i d t + 5 i = 10 Dado que i 0 = 2 e d i 0 d t = 4 , determine i ( t ) .