Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 55

No circuito da figura, a chave esteve na posição 1 por um longo tempo antes de ser movida para a posição 2 em t = 0 . Determine:

  1. v ( 0 + ) ,   d v ( 0 + ) d t
  2. v ( t ) para t ≥ 0 .

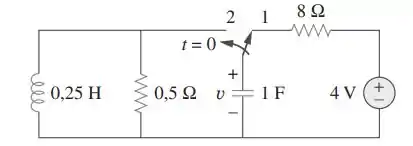
Passo 1

Para t > 0 teremos:

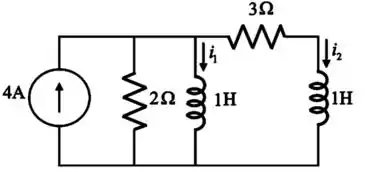
Em seguida, vamos passar os elementos para o domínio de Laplace e desenhando o circuito para facilitar a visualização:

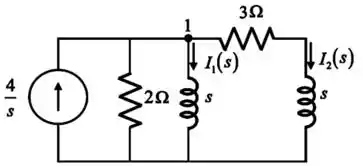
Passo 2

Utilizando a análise nodal no nó 1, teremos uma expressão para V 1 ( s ) :

4 s = V 1 ( s ) 2 + V 1 ( s ) s + V 1 ( s ) s + 3

V 1 ( s ) = 8 ( s + 3 ) s 2 + 7 s + 6

Passo 3

A partir disso, sabemos qual é a corrente no indutor:

I 1 ( s ) = V 1 ( s ) s = 1 s [ 8 ( s + 3 ) s 2 + 7 s + 6 ]

Passo 4

Separando em frações parciais teremos:

I 1 ( s ) = 1 s [ 8 ( s + 3 ) s 2 + 7 s + 6 ] = A s + B s + 1 + C s + 6

Agora basta encontrar A ,   B   e   C   :

A = 4

B =   - 3.2

C =   - 0.8

Daí, substituindo, teremos:

I 1 ( s ) = A s + B s + 1 + C s + 6

Por Laplace utilizando a tabela de transformadas, teremos:

i ( t )   =   4 - 3.2 e - t - 0.8 e - 6 t   A , para t > 0.

Resposta

i ( t )   =   4 - 3.2 e - t - 0.8 e - 6 t   A , para t > 0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine i 0 ( t ) para t0 no circuito da figura.
Determine a tensão v o ( t ) no circuito da figura por meio da transformada de Laplace
Determine vo(t) no circuito da Figura 16.82 se vx(0) = 2 V e i(0) = 1 A.
Determine a transformada de Laplace da tensão mostrada na figura. Usando o valor de v s ( t ) no circuito mostrado na figura, determine o valor de v o ( t ) .
Considere o circuito RLC mostrado na figura e determine a resposta completa se v ( 0 ) = 2V quando a chave é fechada.