Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 45
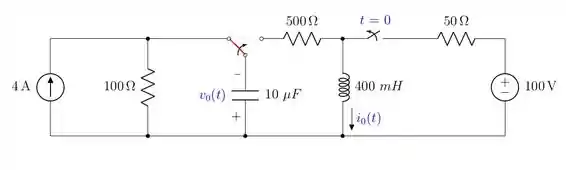
O circuito mostrado na Figura P8.45 esteve em funcionamento por um longo tempo. Em , as duas chaves passam para as novas posições mostradas na figura. Determine
a) para .
b) para .
Passo 1
Faaaaaaaaaaaaaala, pessoal! Tudo beleza? Vamos resolver essa questão que possui um chaveamento “diferenciado”. Temos que saber primeiramente o comportamento do circuito antes do chaveamento. Como explicitado no enunciado, a chave ficou aberta um tempão, o que significa que o capacitor vai se comportar como um circuito aberto e o indutor como um curto-circuito. Sendo assim, vamos analisar cada um dos lados do circuito acima.
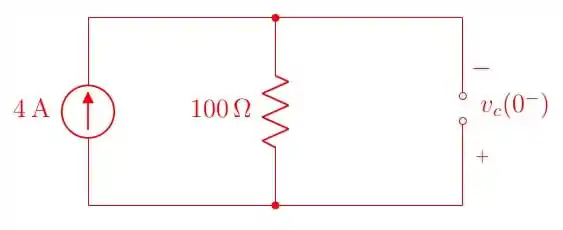Esse circuito fornece a tensão inicial no capacitor que pode ser obtido pela Lei de Ohm:
Esse é o outro circuito onde o ramo mais grosso representa o indutor em regime permanente. Assim,
Uma vez encontradas essas grandezas, vamos estudar o comportamento do circuito para :
Além disso,
Conhecendo as duas frequências, vamos compará-las para sabermos o tipo de resposta do circuito. Como , temos que a resposta do circuito é superamortecida. Assim, suas raízes são
Passo 2
A corrente vai ter a seguinte forma
Vamos começar estudando a corrente quando :
Como vimos lá no começo que a corrente inicial no indutor valia , temos que
Podemos encontrar outra relação derivando a equação da corrente:
Para encontrarmos um valor para essa equação que envolve a derivada da corrente, vamos lembrar que a tensão no indutor é dada por
Para achar o valor de temos que usar a LKT, mas precisamos ter muito cuidado pois nessa situação os chaveamentos já ocorreram e nós teremos o seguinte circuito para analisar:
Perceba que a LKT para o circuito marrom vai nos fornecer:
Voltando para a expressão da derivada da corrente, temos que
Assim, nosso sistema é composto de duas equações:
Resolvendo este sistema, obtemos que
Logo, a corrente tem a seguinte forma:
Passo 3
b)
Para resolvermos este item vamos precisar apenas fazer um pouco de algebrismo. Sabemos que a corrente no indutor é dada por
Como estamos trabalhando com , vamos fazer essa mudança de notação posteriormente. Para resolvermos essa equação, vamos olhar para e como diferenciais. Assim, podemos escrevê-la como
Integrando ambos os lados da equação, vamos obter
Fizemos uma mudança de variáveis apenas por uma questão de formalidade, visto que os limites de integração devem ter uma notação diferente da variável de integração. Assim:
Aqui aplicamos o mesmo princípio da notação, visto que está expressa em função de t. Então:
Neste ponto, é mais vantajoso dividirmos a integral em 2, pois isso facilitaria bastante a manipulação:
Chegamos assim ao final de mais uma questão. Sugiro fazer uma pausa de 10 minutos antes de irmos para a próxima questão porque tenho um pressentimento que ela será um pouco longa!
Resposta
a)
b)