Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 53

No circuito da figura, a chave esteve na posição 1 por um longo tempo antes de ser movida para a posição 2 em t = 0 . Determine:

  1. v ( 0 + ) ,   d v ( 0 + ) d t
  2. v ( t ) para t ≥ 0 .

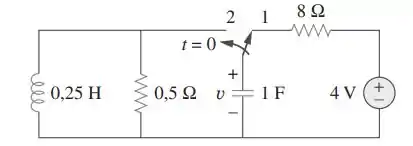
Passo 1

Vamos começar passando os elementos para o domínio de Laplace e desenhando o circuito para t < 0 (regime permanente) para facilitar a visualização:

Note que em regime permanente o indutor é um curto circuito e o capacitor é um circuito aberto.

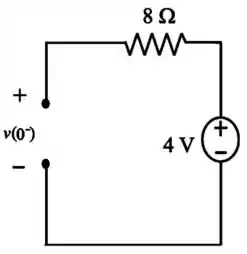
Passo 2

Como o capacitor não permite mudanças repentinas na tensão, então:

v ( 0 - ) = v ( 0 + ) = v ( 0 ) = 4   V

Passo 3

Agora, faremos para t > 0 no domínio de Laplace e com as condições iniciais:

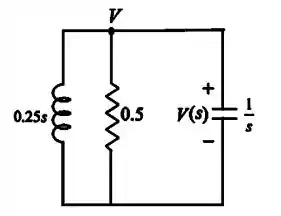
Passo 4

Agora, basta calcular a derivada da tensão.

Aplicando a lei das tensões de Kirchhoff no nó V :

C d V c ( 0 + ) d t + V ( 0 + ) 0.5 + i L ( 0 + ) = 0

d V c ( 0 + ) d t =   - 8 V

d v ( 0 + ) d t =   - 8 V

Passo 5

Na letra b, temos o circuito para t > 0 no domínio de Laplace:

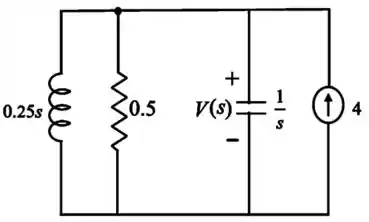
Passo 6

Utilizando a análise nodal no nó, temos:

V ( s ) 0.25 s + V ( s ) 0.5 + V ( s ) 1 s - 4 = 0

V ( s )   = 4 s s 2 + 2 s + 4

Passo 7

Como a equação é mais simples, não precisamos utilizando o método das frações parciais, então, por Laplace utilizando a tabela de transformadas, teremos:

e - a t f ( t ) ↔ F ( s + a )

u ( t ) ↔ 1 s

t ↔ 1 s 2

e - a t c o s ω t ↔ s + a ( s + a ) 2 + ω 2

e - a t s i n ω t ↔ ω ( s + a ) 2 + ω 2

Chegaremos em:

V ( s )   = 4 s s 2 + 2 s + 4 = 4 ( s + 1 ) ( s + 1 ) 2 + ( 3 ) 2 - 1 3 4 × 3 ( s + 1 ) 2 + ( 3 ) 2

Fazendo a inversa, chegamos à:

v ( t )   =   4.618 e - t c o s ( 1.732 t + π 6 ) V , para t > 0.

Resposta

  1. d v ( 0 + ) d t =   - 8 V
  2. v ( t )   =   4.618 e - t c o s ( 1.732 t + π 6 ) V , para t > 0.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

101- Concretize a função de transferência V o s V s ( s ) = - s s + 10 Usando o circuito da Figura 16.110 . Seja Y 1 = s C 1 ,Y 2 = 1 / R 1 , Y 3 = s C 2 . Adote R 1 = 1k Ω e determine C 1 e C 2 .
97- Um sistema é formado pela conexão em cascata de dois sistemas, conforme exibido na Figura 16.106 . Dado que as respostas dos sistemas a um impulso são h 1 t = 3 e - t u t ,h 2 = e - 4 t u ( t ) (
102- Sintetize a função de transferência V o s V e n t s = 10 6 s 2 + 100 s + 10 6 Usando a topologia da Figura 16.111 . Seja Y 1 = 1 / R 1 , Y 2 = 1 / R 2 , Y 3 = s C 1 , Y 4 = s C 2 . Adote R 1 = 1
88- Desenvolva as equações de estado para o circuito da Figura 16.102 .
90- Desenvolva as equações de estado para o circuito mostrado na Figura 16.104