Mostre que, no caso geral, a função de rede na figura do Prob. 15.1 é dada por
Desta forma, por comparação com (15.22) e (15.25), mostre que o circuito é um filtro passa-faixa com frequência de ressonância , largura da faixa e índice de mérito . Mostre também que o ganho do filtro, definido como seu valo de pico da amplitude, é dado, neste caso, por .
Passo 1
Deixe-me adivinhar... Vc ficou assim com tanta coisa que a questão pediu:

Se preocupe não que é mais simples do que vc imagina haha
Primeiramente, o circuito que a questão está mencionando é este:
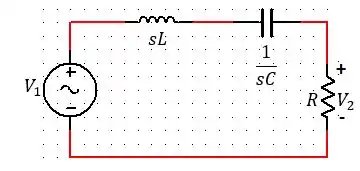
Pela Lei de Ohm a corrente nesse circuito será:
Assim, é dado por:
Passo 2
Nesse sentido, percebemos que tem o formato de:
Logo, temos que:
Passo 3
O índice de mérito é dado por:
Substituindo os valores de e , temos:
Passo 4
Por fim, temos que o ganho é dado por:
Prooonto!! Viu? Simples! Só ir substituindo!! ;)