Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 32

Mostre que a função de transferência V 2 / V 1 é dada por

H ( s ) = V 2 ( s ) V 1 ( s ) = 1 R 1 s s 2 + 1 R 2 s + 1 R 3

Calcule R 1 , R 2 e R 3 de forma a que a funçăo de transferėncia seja idéntica á do Prob. 15.1.

Passo 1

E aí gurizada tudo belezinha? O enunciado pede que a gente Mostre que a função de transferência V 2 / V 1 é dada por

H ( s ) = V 2 ( s ) V 1 ( s ) = 1 R 1 s s 2 + 1 R 2 s + 1 R 3

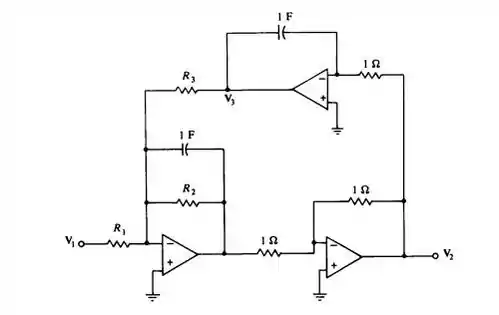
Fazendo o esboço podemos calcular, então vem comigo 😊

- V 1 R 1 = V 2 R 2 + V 2 1 / s + V 2 / Δ R 3 ⇒ V 1 R 1 = V 2 R 2 + V 2 s + V 2 s R 3

V 1 R 1 = V 2 1 R 2 + s + 1 s R 3 ⇒ V 1 V 2 = R 1 s R 3 + s 2 R 2 R 3 + R 2 s R 2 R 3 ⇒

V 2 V 1 = s / R 1 s 2 R 1 R 2 R 3 + s R 1 R 3 + R 1 R 2 ⇒ V 2 V 1 = s s 2 + s R 2 + 1 / R 3

Resposta

s s 2 + s R 2 + 1 / R 3

Exercícios de Livros Relacionados

Calcule a admitância Y ( s ) vista pela fonte e coloque seus pólos e zeros. Se a fonte é v g = 4 e - t c o s ⁡ tV , calcule a resposta forçada i
Use o método do Prob. 14.6 para calcular a impedância vista da fonte. e use o resultado para calcular a resposta forçada t
Calcule a representação fatorial V ( s ) e a frequência s de (a) v ( t ) = 5 e - 2 c o s ⁡ 10 t - 30 p ; ( b ) v ( t ) = e - 1 s e n ⁡ 5 t + 45 ∘ ; ( c ) v ( t ) = 2 e - 3 t ( 3 c o s ⁡ 3 t + 4 s e n
Calcule a função de rede V ( s ) / V e ( s ) e use o resultado para calcular a resposta forçada v , se v g = 6 e - 2 t c o s ⁡ 4 tV
Calcule H ( s ) = V ( s ) / V g ( s ) e use o resultado para calcular a resposta forçada v , se v q = e 2 t c o s ⁡ 2 tV