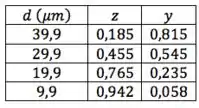
Foram os seguintes resultados obtidos na elutriação de de um pó industrial com água a , numa vazão de :
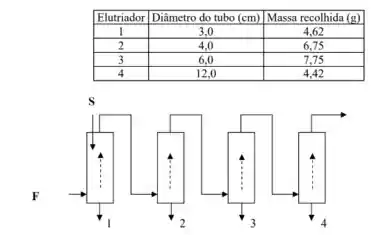
Determinar a distribuição granulométrica da amostra, sabendo-se que e .
Passo 1
Nessa questão, nosso objetivo é determinar a distribuição granulométrica da amostra; nem precisamos calcular a curva , basta entregar uma tabela relacionando diâmetros e . Mas vamos por partes.
Primeiro de tudo, vou trabalhar no CGS, daí sempre que aparecer algo que não está no CGS eu vou convertendo. A vazão é constante em todos os elutriadores, ; o que muda de um elutriador para outro a velocidade média do fluido, já que a área transversal dos elutriadores muda, já que o diâmetro muda.
Daí:
Como , podemos montar uma tabela com os valores de para cada elutriador.
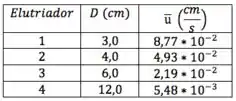
Repara que, conforme o diâmetro do elutriador vai aumentando, como a vazão é constante, a velocidade média do fluido vai diminuindo, permitindo que partículas menores sedimentem, já que elas têm velocidades terminais menores. O que eu quero dizer com isso é que, no primeiro elutriador, vamos ter partículas maiores; no último, as menores. Dessa forma, essa massa de recolhida no primeiro elutriador é de partículas maiores que a partícula que tem e o somatório das massas dos elutriadores 2, 3 e 4 é de partículas com diâmetro menor que essa tal partícula que tem .
Mas antes de começar as contas, precisamos de todos os dados; sobre as partículas, sabemos que e , mas, sobre o fluido, apenas sabemos que este é água à . Precisamos procurar as propriedades. Procurando: e .
Passo 2
Precisamos determinar que são as partículas que têm essas velocidades terminais que aparecem na nossa tabela. Como não sabemos o regime de sedimentação, vamos utilizar Coelho e Massarani e, como temos e queremos , vamos por:
Achado , usamos, para achar o :
E, para isso, precisamos de e , que vão ser os mesmos para todas as partículas, já que todas possuem a mesma esfericidade, , e seus valores são:
Uma vez obtidos os valores de para cada uma das partículas “limite”, achamos o diâmetro delas usando a definição de :
Calculando pra cada uma delas:
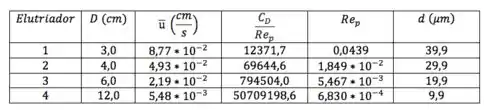
Passo 3
Agora precisamos relacionar esses diâmetros “limite” com valores de ou . Antes de qualquer coisa, precisamos saber a massa total da amostra, que foi dada: .
No elutriador , sabemos que do foram recolhidas, ou seja, sedimentaram. Essas partículas possuem velocidades terminais maiores que e, consequentemente, , ou seja, está associado com:
E, como :
Para o elutriador , temos que nos atentar que as partículas maiores que são não só as que da massa que sedimenta no elutriador , mas a que sedimenta no primeiro também! Daí:
Da mesma forma, para o , as partículas maiores que são as da massa que sedimenta nos elutriadores e . Daí:
Para o , as partículas maiores que são as da massa que sedimenta nos elutriadores 3 e . Daí:
Resposta