Uma mistura de galena () e sílica () será submetida a elutriação gravitacional por uma corrente de água que escoa a uma velocidade de na Temperatura de . A mistura tem 30% de massa de galena e a seguinte análise granulométrica com peneiras padronizadas:

Se a distribuição de tamanhos anterior se aplica tanto à galena quanto à sílica, pede-se:
- Calcule as percentagens ponderais da galena, originalmente presente na alimentação, que irão para o topo e fundo do elutriador.
- Calcule a fração ponderal de galena nessas correntes (base seca).
Passo 1
Nessa questão, precisamos encontrar o quanto de galena e sílica foi para o topo e fundo do elutriador, certo?
Mas como fazer isso a partir da distribuição de tamanho (DT) dada?

Nesse tipo de problema, já temos a velocidade e precisamos encontrar o diâmetro para cada amostra que acima dele a partícula vai para o fundo e abaixo dele a partícula vai para o topo! Isso tem que ser feito para cada um dos sólidos 😊 E depois relacionamos com a DT.
Vamos organizar os dados que a questão forneceu:
Foi dado tanto o da sílica quanto da galena, conseguimos achar o de cada uma.
Outra coisa, já que não foi dada a esfericidade e não temos como calcular, vamos assumir que a partícula é esférica e atende todas as restrições de stokes, beleza? E isso significa que podemos fazer mais uma simplificação:
Só mais uma coisinha, foi dado que a temperatura era de , então podemos pegar em tabelas as propriedades da água nessa temperatura:
Passo 2
Vamos começar então calculando o diâmetro de stokes para cada um dos materiais. Para isso, vamos isolar o diâmetro da fórmula de velocidade de stokes.
E repara que só temos a velocidade do fluido, que é diferente da velocidade das partículas, mas sabemos que que elas tem a seguinte relação:
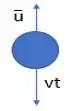
Então se a gente achar o diâmetro de stokes para a partícula exatamente na velocidade do fluido, vamos saber que a partir daquele diâmetro ela vai descer e abaixo dele vai subir! Então, estamos estudando o caso que:
Para a galena:
Para a sílica:
Passo 3
Agora, vamos avaliar a distribuição de tamanho de partícula e relacionar com esses diâmetros que calculamos.
Lembra que como consideramos esféricas igualamos o diâmetro de stokes e da peneira, então não precisamos converter eles para compará-los! Então, o diâmetro da galena, ,fica ali entre e . E o diâmetro da sílica, , fica entre e

Então, podemos fazer uma interpolação para descobrir o relativo a cada diâmetro.
Para a Galena:
Para a Sílica:
LEMBRETE: O valor de representa a amostra menor que dado diâmetro então esse está relacionado com as partículas que vão subir!
Passo 4
Agora, vamos assumir uma base mássica de cálculo.
Como temos de galena, podemos definir a massa de galena e massa de sílica.
Então, vamos definir a massa de sílica e galena que é menor /maior que o diâmetro calculado para cada uma?
Fazendo da mesma forma para sílica:
Passo 5
Já calculamos quase tudo, então para resolver a letra a) precisamos definir a percentagem de galena (EM RELAÇÃO À ALIMENTAÇÃO) no topo e fundo.
Repara que a porcentagem no topo é o mesmo valor que calculamos do , isso ocorre pois a curva representa valores menores ( e tem a mesma densidade, já que estamos falando só da galena) que um dado diâmetro, então como são menores são mais leves e vão para o topo!!
Passo 6
Na letra b), precisamos calcular a fração ponderal de galena nas correntes de saída! Então, vamos calcular a massa total dessas saídas:
Então, a massa total do topo:
E a do fundo:
Logo, bora calcular as percentagens de galena no topo e fundo!