Pretende-se tratar uma corrente industrial com de ar a e contendo finos de carvão (densidade: e esfericidade: ), utilizando-se o seguinte sistema (elutriador e câmara de poeira em série):
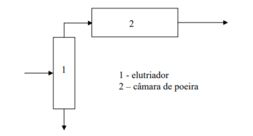
Sabendo-se que o elutriador captura todas as partículas maiores que e que a eficiência de separação de uma partícula de na câmara de poeira é igual a , pede-se:
- O diâmetro do elutriador e sua eficiência total de separação.
- A eficiência total de separação da câmara de poeira.
- A eficiência global do processo.
Dados:
e
Dica: Uma suspensão que passa por um equipamento de separação tem, obviamente, sua distribuição de tamanhos de partícula alterada, uma vez que o equipamento irá capturar parte das partículas presentes, preferencialmente as mais grossas. Se o separador é ideal e a distribuição granulométrica é dada pelo modelo GGS, o único parâmetro do modelo que sofre alteração é o tamanho da maior partícula presente, isto é, o muda e o não.
Passo 1
Temos dois equipamentos em série, um elutriador e uma câmara de poeira, sendo que o overflow do elutriador é que vai pra a câmara de poeira.
As duas primeiras perguntas do enunciado focam nos equipamentos em separado, já o último item pede a eficiência global, daí vamos ter que usar:
Com:
Em que é o elutriador e a câmara de poeira.
AHH! Uma coisa importante: o enunciado NÃO deu a densidade do gás, mas deu as condições dele
e 1 atm
Assumindo gás ideal, vale:
Podemos escrever o número de moles como , com sendo massa de gás e sendo a massa molecular média. Rearranjando:
Trabalhando no CGS e usando em Kelvin:
Passo 2
a) O diâmetro do elutriador e sua eficiência total de separação.
Nos foi informado que o elutriador deverá capturar todas as partículas maiores que . Daí, vamos analisar o limite, que é a partícula de . Para ela:
Daí, achando , achamos . Como:
Com sendo a vazão volumétrica e a área transversal do elutriador.
Poderemos achar o diâmetro do elutriador, já que temos
.
Ok! Então bora encontrar . Vamos ter que usar as correlações de Coelho e Massarani. Como temos e queremos :
Usando tudo no CGS:
Agora, para achar , usamos:
Mas, primeiro, temos que calcular e , que ainda não temos. O enunciado deu que a esfericidade vale .
Voltando:
Usando a definição de Reynolds:
Passo 3
Agora que temos e sabemos que
Podemos determinar o diâmetro do elutriador:
Usando no CGS, também, pra compatibilizar as unidades:
Daí:
Passo 4
Ainda falta calcular a eficiência total no elutriador, mas, antes, a gente tem que ver . No elutriador vale:
E, nessa questão:
Agora, pra achar a eficiência total, temos que integrar:
E repara duas coisas:
1. A integral é em termos de e NÃO de , daí temos que determinar o do , que será o divisor dos intervalos
2. é definida em dois intervalos, daí a integral também terá de ser dividida
Vamos um por um então. Usando a equação de fornecida:
Para
Daí ficamos com:
E a integral fica:
Passo 5
b) A eficiência total de separação da câmara de poeira.
Agora partimos pra câmara de poeira. Vamos com calma. Primeiro de tudo, bora lembrar a definição de eficiência:
Massss essa entrada aí é a entrada do equipamento. O que entra na câmara de poeira NÃO é o que entra lá no começo e sim o que NÃOOOO foi coletado no elutriador, isto é:
Como , o que entra na câmara é do alimentado inicialmente.
E com isso achamos o denominador.
Para achar o numerador, teremos que ver quanto é coletado a câmara de poeira. Usando a mesma equação pra , o que vai mudar são os limites de integração pois na câmara de poeira só estão entrando partículas entre e , certo? As maiores de já foram coletadas no elutriador.

Em termos de , isso fica:
Daí a entrada da câmara de poeira compreende:
E para achar o que captura nela , é só integrar em , usando a equação de original, mas usando esses limites aí:
Mas, antes, temos que saber quem é o , certo?
Para câmara de poeira, vale:
Não temos nenhuma informação das dimensões da câmara e o exercício não é de dimensionamento... NÃO é conveniente trabalhar com essas equações, dessa forma; é melhor trabalhar com ela adimensional:
O que sabemos é que a eficiência de separação de uma partícula de na câmara de poeira é igual a . Repara que ele está falando de , pois amarrou eficiência para um dado diâmetro.
Usando a equação de para , conseguimos achar :
Mas os limites de envolvem , né? Precisamos achá-lo. Vimos, na teoria, que usando essa fórmula aí de dá pra chegar em:
Daí:
Portanto:
Em termos de :
Passo 6
Agora é só integrar. Como está definida em dois intervalos, dividimos a integral em dois intervalos também:
Repara que ainda temos que colocar em função de . Estamos considerando da alimentação original o tempo todo então é ele que vamos usar agora também:
Daí:
Integrando:
E esse é o numerador! Repara que chamei de e não de . Esse valor é quanto da alimentação original é capturado na câmara de poeira, mas o enunciado pede qual a eficiência da câmara de poeira, dai, quanto é capturado nela em relação ao que entra nela. Voltando pra fórmula que vimos no outro passo:
Eu prefiro seguir por esse caminho que eu fiz, mudando os limites de integração e mantendo a expressão de , mas outra opção seria usar aquela dica do enunciado e mudar a expressão de , mantendo os limites e .
Passo 7
c) A eficiência global do processo.
Já temos as eficiências totais e por tamanho de cada equipamento, mas agora temos que calcular a eficiência global do processo. Pra isso, é só usar:
Com:
O lance é que vamos ter que dividir em intervalos porque os ’s estão definidos em intervalos.
Bora começar lembrando :
Ou seja, para :
Para
E vimos que
Daí a integral fica:
Resposta
- e