Encontre a solução da Equação de Laplace na faixa semi-infinita , , que satisfaz as condições de contorno
E a condição adicional de que quando
Passo 1
Esse problema tem um detalhe diferente, olha só as condições que temos:
Como nos outros problemas, nós ainda temos 4 condições para a Equação de Laplace. Mas aqui, uma delas não nos dá nem o valor de em um ponto nem a sua derivada, nós da um limite! WTF.
Isso acontece porque, como o problema diz, não temos um retângulo, mas uma faixa semi-infinita, ela é “finita” na direção e “infinita’ na direção , olha só:
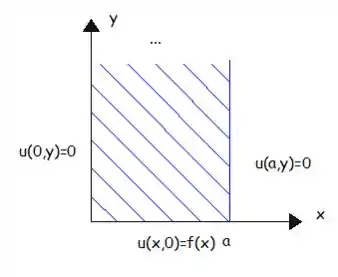
Por isso a 4ª condição não é um valor na borda, mas um limite!
Por enquanto nós vamos resolver o problema da mesma forma que temos feito, depois nos preocupamos com essa condição esquisita, ok?
Passo 2
Beleza, agora vamos fazer, como sempre, a separação de variáveis.
Procuramos uma solução do tipo . Como essa solução deve satisfazer a Equação de Laplace, temos:
Agora nós passamos tudo que tem para um lado e o que tem para o outro:
Como essa igualdade vale para todo e para todo , essas razões devem ser iguais a uma constante. Separando em duas equações, temos:
Aplicando a separação de variáveis para as condições homogêneas do problema (a função e o limite nós deixamos para depois):
Então, temos o seguinte:
Não está faltando uma condição para ? Calma, vamos chegar lá!
Passo 3
Resolver o problema que tem duas condições (de contorno)
Como a função é a que possui duas condições de contorno, vamos resolver primeiro o problema em , temos:
Temos a seguinte equação característica:
Vamos ver as soluções caso a caso agora.
Caso 1: . Ou seja, o que está dentro da raiz é positivo. Nesse caso, . As soluções são do tipo:
Agora vamos usar as condições de contorno:
Isso nos dá
Substituindo esses valores na nossa solução geral, temos
Mas isso não nos ajuda em nada! Essa é a solução trivial, que não nos interessa. Portanto, esse caso, , não nos dá soluções para a EDO.
Caso 2: . Nesse caso, . As soluções são do tipo:
Agora vamos usar as condições de contorno:
Isso nos dá
Substituindo esses valores na nossa solução geral, temos
Novamente, a solução trivial, que não nos ajuda em nada. Beleza, vamos ver o 3º caso agora!
Caso 3: . Ou seja, o que está dentro da raiz é negativo. Nesse caso, . As soluções são do tipo:
Substituindo
Agora vamos usar as condições de contorno:
Isso nos dá
Agora vamos com calma! Se tivermos , a solução é a trivial , que não nos interessa. Então, para essa igualdade ai em cima ser verdadeira, precisamos que o seno seja zero.
O seno se anula em , , ... , múltiplos inteiros de . Logo, podemos dizer que:
As soluções do 3º caso são então do tipo:
Passo 4
Tendo os valores de , resolver a outra EDO
Beleza, agora temos que resolver o problema em , temos:
A equação característica dessa EDO é a seguinte:
Já vimos que , não é? Quando encontramos seu valor no passo anterior. Então, as soluções dessa EDO são do tipo:
Como nós já vimos, é usual escrever essa resposta em função de e . Mas nós vamos ter que tomar o limite de para satisfazer as condições do problema, e analisar o limite das exponenciais é muito mais simples, né? Então vamos escrever a solução em exponenciais mesmo.
Temos o seguinte agora:
Para sumir com esses coeficientes e , precisamos aplicar a condição:
OBS: como é uma função que oscila, o limite de depende apenas da parte que tem !
Agora repara que, como , o limite desse 1º termo é infinito quando . Já o limite do 2º termo é zero, porque o expoente é negativo.
Então, para que , precisamos sumir com esse 1º termo, o que nos leva a
Certo? Temos então:
Nós não escrevemos o porque, como já vimos, autovetores são escritos sem o coeficiente que os multiplica.
Passo 5
Precisamos escrever como série e achar os coeficientes da série
Como as combinações lineares de também são soluções do problema, temos que:
Agora vamos usar a condição que faltou:.
Como essa é uma Série de Fourier de senos, fazendo uma extensão ímpar de , podemos dizer que:
Repare que o período da extensão é , não . Por isso apareceram esses ’s na integral, tome cuidado. O veio do denominador do seno.
Dessa forma, encontramos os coeficientes da série e substituímos em
Resposta
Onde