(Adaptado) Ar a escoa com uma vazão de através de canais com de comprimento usados para resfriar um molde metálico de alta condutividade térmica. Suponha que o escoamento esteja fluidodinâmica e termicamente plenamente desenvolvido.
Considere o ar escoando em um canal segmentado em seis seções triangulares de lado . Determine o calor transferido para o ar, quando a temperatura do molde é de .
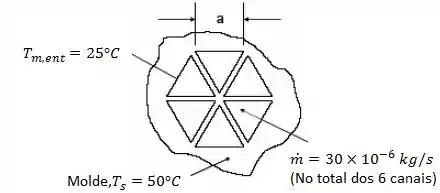
Passo 1
Como não temos a temperatura de saída e este é um problema com temperatura superficial constante, vamos precisar chutar uma temperatura de saída para definir as propriedades do fluido.
Como temos uma temperatura de entrada igual a e o molde está a uma temperatura de , vamos chutar uma temperatura de saída de , bem próximo da temperatura do molde.
Assim, a média das temperaturas de entrada e saída será:
De acordo com a tabela A.4 do Incropera, para o ar a esta temperatura, temos que:
Agora estamos prontos pra seguir em frente.
Passo 2
A taxa de transferência de calor será dada por:
Onde a temperatura de saída é dada por:
Pra calcular o coeficiente convectivo, vamos precisar do número de Nusselt:
Então vamos calculá-lo.
Passo 3
Para calcular o número de Nusselt, precisaremos do número de Reynolds, dado por:
Onde o diâmetro hidráulico é dado por:
Além disso, como estamos calculando o número de Reynolds em relação para um dos canais, precisamos dividir o fluxo mássico por 6. Dessa forma, o fluxo mássico através de cada canal será:
Substituindo os valores:
Opa! Estamos no regime laminar. Assim, pela tabela na teoria, considerando o caso de temperatura superficial constante, o número de Nusselt será:
Assim, o coeficiente convectivo será:
Passo 4
A temperatura média de saída do fluido será:
Substituindo os valores:
Passo 5
Finalmente, a taxa de transferência de calor será:
![]()