(Adaptado) Um fluido refrigerante escoa através de um canal retangular (galeria) no interior do corpo de um molde que é utilizado para produzir peças metálicas.
As dimensões da galeria são e , e a vazão volumétrica do fluido é de . A temperatura do refrigerante é de e a parede do molde encontra-se a uma temperatura aproximadamente uniforme de .
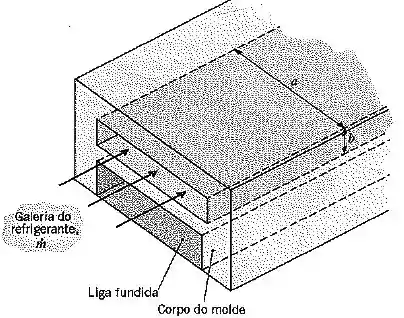
Para minimizar os problemas de corrosão no molde, que é uma peça de custo elevado, é comum se utilizar como fluido refrigerante o etilenoglicol, no lugar de água de processo. Compare os coeficientes convectivos da água e do etilenoglicol nesta aplicação.
Calcule o coeficiente convectivo para a água e para o etilenoglicol.
Passo 1
Para determinar as propriedades dos fluidos, vamos supor que a temperatura de saída do fluido seja igual à temperatura do molde. Dessa forma, a média da temperatura de entrada e saída será:
De acordo com a tabela A.6 do Incropera, para as propriedades da água, temos que:
E, de acordo com a tabela A.5 do Incropera, para as propriedades do etilenoglicol, temos que:
Passo 2
Vamos começar resolvendo o problema para a água.
Pra calcular o coeficiente convectivo, vamos precisar do número de Nusselt, se liga:
Para calcular o número de Nusselt, precisaremos do número de Reynolds, dado por:
Onde o diâmetro hidráulico é dado por:
Além disso, a velocidade média do fluido é dada por:
Substituindo os valores:
Opa! Estamos no regime turbulento. Assim, pela tabela na teoria, podemos usar a seguinte relação:
Assim, o coeficiente convectivo será:
![]()
Passo 3
Repetindo os cálculos para o etilenoglicol, temos que o número de Reynolds é dado por:
Opa! Como estamos novamente no regime turbulento, vamos utilizar a mesma correlação para o número de Nusselt.
Assim, o coeficiente convectivo será:
![]()