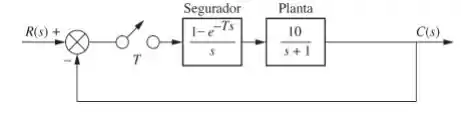
Determine a faixa de período de amostragem, , que tornará o sistema mostrado abaixo estável, e a faixa que o tornará instável.
Passo 1
Para determinar a estabilidade do sistema digital primeiro devemos encontrar a função de transferência em malha fechada dele no plano . Para isso, não podemos encontrar a função de transferência no plano e depois aplicar a transformada .
A abordagem correta na verdade é encontrar a função de transferência em malha aberta no plano , aplicar a transformada , encontrando a função de transferência em malha aberta no plano e com ela encontrar a função de transferência em malha dechada no plano .
Então vamos lá, primeiro de tudo vamos achara a função de transferência em malha aberta no plano :
Passo 2
Agora aplicamos a transformada para encontrar :
Manipulando um pouco temos:
Como pela definição temos que:
Podemos fazer:
Portanto:
Passo 3
Para fazer a transformada vamos aplicar a divisão em frações parciais:
Olhando uma tabela de transformada teremos:
Portanto:
Simplificando:
Fazendo o MMC e juntando tudo:
Passo 4
Com a função de transferência em malha abreta podemos encontrar a função de transferência em malha fechada, :
Portanto:
Multplicando em cima e embaixo por teremos:
Passo 5
Para que o sistema seja estável, as raízes da equação característica devem estar dentro da circunferência de raio unitário com centro na origem. A equação característica para o sistema é o denominador da função de transferência, portanto:
Como é um polinômio de primeira ordem, terá apenas uma raiz, que será:
Ou seja, para que o sistema seja estável é necessário que:
Passo 6
Vamos primeiro encontrar o valor de que torna a raíz :
Aplicando logaritmo em ambos os lados:
E agora, vamos ber qual valor de faz com que a raíz seja :
Aplicando logaritmo em ambos os lados:
Resposta
Portanto o sistemas é estável em e instável em .