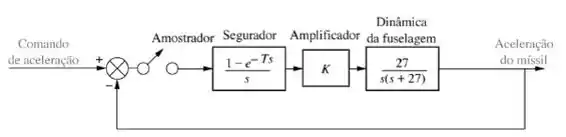
O míssil mostrado na figura abaixo pode ser controlado aerodinamicamente através de torques gerados pela deflexão de superfícies de controle no corpo do míssil. Os comandos para defletir essas superfícies de controle vêm de um computador que utiliza dados de rastreamento em conjunto com equações de guiamento programadas paradeterminar se o míssil segue a trajetória. As informações provenientes das equações de guiamento são utilizadas para desenvolver comandos de controle de voo para o míssil. Um modelo simplificado é mostrado abaixo. Nesse caso o computador executa a função de controlador utilizandoas informações de rastreamento para desenvolver comandos de entrada para o míssil. Um acelerômetro no míssil detecta a aceleração real, a qual é realimentada para o computador. Obtenha a função de transferência digital em malha fechada para esse sistema e determine se o sistema é estável para período de amostragem .
Passo 1
Para determinar a estabilidade do sistema digital primeiro devemos encontrar a função de transferência em malha fechada dele no plano . Para isso, não podemos encontrar a função de transferência no plano e depois aplicar a transformada .
A abordagem correta na verdade é encontrar a função de transferência em malha aberta no plano , aplicar a transformada , encontrando a função de transferência em malha aberta no plano e com ela encontrar a função de transferência em malha dechada no plano .
Então vamos lá, primeiro de tudo vamos achara a função de transferência em malha aberta no plano :
Passo 2
Agora aplicamos a transformada para encontrar :
O ganho como é uma constante pode vir pra fora da transformada:
Manipulando um pouco temos:
Como pela definição temos que:
Podemos fazer:
Portanto:
Passo 3
Para fazer a transformada vamos aplicar a divisão em frações parciais:
Olhando uma tabela de transformada teremos:
Portanto:
Simplificando:
Faznedo o MMC e juntando tudo:
Botando em evidência na segunda parte:
Substituindo:
Passo 4
Com a função de transferência em malha abreta podemos encontrar a função de transferência em malha fechada, :
Portanto:
Multplicando em cima e embaixo por teremos:
Passo 5
Agora que finalmente temos a função de transferência em malha fechada e no domínio , podemos determinar a estabilidade. Para isso precisamos olhar para a equação característica da função de transferência, isto é, o polinômio do denominador:
Expandindo a equação característica:
Para que o sistema seja estável, as raízes dessa equação devem pertencer ao ciclo unitário, ou seja, (ter módulo menor que 1).
Como é um polinômio de segunda ordem, vamos aplicar Bhaskara:
Para saber se essas raízes estão dentro do círculo unitário, basta extrair o módulo delas:
Como o módulo é menor que , as raízes se encontrar dentro do círculo de raio unitário e o sistema é estável.
Resposta
Sistema estável.