Um capilar contém acetona, cujo nível distancia-se do topo a . O capilar é mantido a e , enquanto que uma corrente de ar seco escoa sobre o topo do tubo. Após de operação, o nível do líquido cai para a mais de corrente de ar. Sabendo que a pressão de vapor da acetona a é , determine o seu coeficiente de difusão no ar seco.
Dado: ;
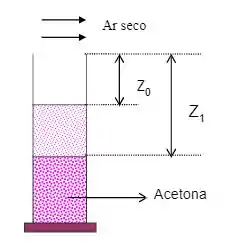
Passo 1
Fala aí! Vamos resolver esse probleminha aí!
O enunciado quer que a gente descubra coeficiente de difusão no ar seco, e nos deu as seguintes informações:
Pra achar o coeficiente de difusão, podemos usar a seguinte equação:
Opa! Mas tá faltando gente aí, né? Vamos encontrar quem está faltando!
Passo 2
Vamos começar encontrando , assim olha só:
Substituindo os valores, temos:
Vamos ter então:
E considerando que no topo está presente ar puro, então:
Agora encontrando a concentração:
Usando a constante dos gases como , e substituindo os valores, temos:
A concentração será:
Passando ele para as unidades corretas, vamos ter:
Beleza! Agora que temos tudo que precisamos, partiu achar o !
Passo 3
Agora vamos voltar lá na equação e substituir nossos valores:
Vamos ficar com:
Uhul! Show de bola!