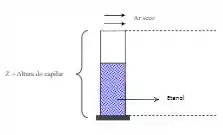
Um capilar está semipreenchido com de etanol. Assume-se que o ar seco contido no interior do capilar esteja estagnado a e . Determine a altura de capilar sabendo que houve um desnível do líquido de no final de .
Dados: ,

Passo 1
Partiu resolver mais uma questão!
Esse enunciado quer que a gente descubra a altura do capilar () e nos deu os seguintes dados:
Além disso o enunciado da pra gente também uma forma de encontrar o , usando a tabela que foi dada, vamos achar então:
Substituindo os valores:
A pressão será então:
Passo 2
Olha só, pra achar essa altura a gente pode usar a equação do tempo em um regime pseudo-permanente, essa aqui olha:
Tá faltando alguns termos ainda, então vamos descobrir eles:
Substituindo os valores, temos:
Vamos ter então:
E considerando que no topo está presente ar puro, então:
Agora vamos encontrar a concentração que também está faltando:
Usando a constante dos gases como , e substituindo os valores, temos:
A concentração será:
Passando ele para as unidades corretas, vamos ter:
Show! Temos tudo que precisamos, partiu achar o !
Passo 3
Agora vamos voltar lá na equação do tempo e substituir nossos valores:
Ajustando esse cara aí, vamos ficar com:
Conseguimos!!