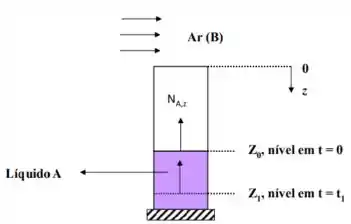
A célula de Arnold é um dispositivo que, de forma simples, permite a medição de coeficientes de difusão mássica. Na figura a seguir, é mostrado um esboço da célula.
- Determine a difusividade mássica de clorofórmio (A) no ar (B), sabendo que, em um experimento com uma célula de Arnold, em horas (), a distância entre a superfície do clorofórmio e do topo da célula passou de ( ) para ( ). Considere que no topo da célula escoava ar puro, ou seja, , e que na superfície do clorofórmio as condições eram de saturação. A temperatura e a pressão mantiveram-se constantes e iguais a e , respectivamente. A pressão de vapor do clorofórmio nessa temperatura é igual a . Apresente o resultado da difusividade em utilizando o mesmo número de algarismos significativos empregados para representar a distância .
- Qual é a característica do processo que permite a adoção de regime pseudo-estacionário na sua modelagem?
Dados: , ,
Passo 1
Fala aí! Vamos resolver essa questão juntinhos, show? Partiu!
Antes de olhar para todos os dados, vamos começar observando a imagem, beleza?
Temos a célula de Arnold, nela a gente vê um sistema onde o clorofórmio fica dentro de um recipiente aberto, exposto ao ar… Humm… Não temos uma reação química acontecendo, e o fluxo é unidimensional.
A figura também nos indica que primeiro temos uma quantidade de clorofórmio e depois de um certo tempo essa quantidade diminui, indicando uma evaporação, né? Opa! Tudo isso nos permite achar a difusividade pela equação do regime pseudo-estacionário, né? Vamos nessa!!
Agora sim, vamos anotar todos os nossos dados!
Show de bola! Vamos para as continhas!
Passo 2
Bom, lembrando que a equação da difusividade em regime pseudo-estacionário é a seguinte:
Opa! Temos quase tudo, mas ainda tá faltando o , vamos achar ele assim:
Substituindo esses valores, que já foram dados pelo enunciado:
Ficamos então com:
Beleza! Agora vamos achar nossa difusividade! Substituindo nossos valores:
A difusividade será então:
Show!
Passo 3
Agora só falta a letra b, né?
Bom, praticamente respondemos ela no passo 1… haha
O enunciado tá perguntando pra gente qual é a característica desse processo que faz a gente adotar o regime pseudo-estacionário… Olha só, como a gente viu lá no passo 1, temos uma evaporação do clorofórmio que acontece bem devagarinho, e essa taxa de evaporação muito pequena é o que nos indica o regime pseudo-estacionário!
Prontinho! Arrasamos!
Resposta
- A taxa de evaporação muito pequena, do clorofórmio no ar, nos indica o regime pseudo-estacionário.