Condições de Contorno
Produzido por Raphael EloiTeoria
Fronteiras das nossas equações
Fala mestre! Esse tópico é mais tranquilo. Já pode respirar aliviado.
Na verdade, já pode batizar esse tópico como “O Facilitador de Vidas”.
Até agora vimos umas das equações diferenciais mais complicadas de se resolver da história. Tão complicadas que existe um número bem limitado de tipos de problema que conseguimos resolver na mão.
Seria praticamente impossível resolver alguns problemas sem o que vamos ver agora, mesmo usando um computador.
Vamos listar algumas das condições de contorno que podemos aplicar nos nossos escoamentos. Isso vai ajudar a gente a encontrar constantes, desconsiderar algumas partes das equações... Vai ajudar a beça, confia em mim.
Um bom exemplo de condição de contorno são as fronteiras de um escoamento.

Se nossos problemas fossem uma pizza, além de entregues em 30 minutos, as condições de contorno de fronteira seriam as bordas.
Ou seja, são as paredes do nosso volume de controle, mas também são as interfaces entre os fluidos e as entradas e saídas do nosso escoamento.

O encontro entre céu e mar é um ótimo exemplo de encontro de fluidos: ar e água. E isso pode ser uma fronteira no nosso escoamento.
Condições de Fronteira
-Entradas e Saídas:
Todo escoamento precisa de entradas e saídas. E para sabermos como se comporta o escoamento dentro do volume de controle, precisamos saber como ele entrará e como sairá.
Ou seja, conhecemos as condições iniciais de velocidade e pressão, assim como as finais.
-Paredes:
Paredes são todas barreiras sólidas e impermeáveis ao escoamento. Por exemplo o cano por onde passa água na sua casa é uma condição de contorno. Afinal não teríamos escoamento depois da parede do tubo.
Além disso existe a hipótese de não-escorregamento na parede. Isso significa que o fluido adquire a mesma velocidade que a parede, como se a partícula fluida estivesse “colada” na parede. Neste caso:
Comumente a parede está parada em relação ao fluido, ou seja, .
-Interface entre fluidos
A grosso modo funciona como uma parede também. Mas com hipóteses diferentes e que acarretam uma análise muito mais complexa do escoamento.
Por exemplo: é adicionada uma variável chamada elevação da superfície livre, denotada por:
E como deve haver continuidade, as velocidades verticais dos fluidos devem ser iguais a:
Isso é chamado de condição de contorno cinemática.
Uma boa simplificação para esses escoamentos é que em interfaces tranquilas, ou seja, sem variações bruscas de elevação, as condições de pressão são iguais.
No caso do céu e mar, a pressão na interface é , de pressão atmosférica.
Outras condições
-Propriedades constantes:
Essas nós estamos usando direto sem nem saber que são condições de contorno.
A hipótese de que existem escoamentos incompressíveis () é muito utilizada em escoamentos de fluidos, pois retira completamente uma variável das nossas equações. Ela é válida para a maioria dos escoamentos líquidos e alguns tipos de escoamentos gasosos, mas normalmente só líquidos.
Outra é a da viscosidade cinemática() ser constante. Assim como no caso anterior, poucos escoamentos newtonianos tem notável variação da viscosidade, portanto considerá-la constante retira outra variável que poderia nos atrapalhar.
-Aproximações:
Em alguns escoamentos podemos desconsiderar completamente algumas variáveis.
O caso mais comum é o de escoamentos sem atrito. Ou seja, sem parcela viscosa de forças. Isso é muito usado em escoamentos gasosos.
A utilização disso leva às Navier-Stokes tomarem a cara da Equação de Euler, por exemplo:
Acabei de te apresentar as condições que vão facilitar sua vida daqui para frente!

Na hora de começar o exercício, leia o enunciado com atenção buscando quais condições de contorno facilitadoras de vida você pode usar!
Para ficar craque nisso, bora para os exercícios! Pratica aí! 😊
Condições de Fronteira
Outras condições
Exercícios Resolvidos
Exercício Resolvido #1
Concurso Petrobras (Cesgranrio) – Técnico de Operação Júnior - 2017
(Adaptada) Em um escoamento sobre uma placa plana, a velocidade do fluido em contato com a superfície sólida é zero, embora o fluido esteja em movimento. A condição de não escorregamento é uma característica de todos os escoamentos de fluidos
(A) ideais
(B) compressíveis
(C) não newtonianos
(D) viscosos
Passo 1
E aí! Que bom que você veio aqui :D Esse é um exercício de concurso que checa como estamos na teoria. Afinal, a condição de não escorregamento (ou não deslizamento) vale para qual tipo de fluido?
Primeiro, vamos lembrar quem é essa condição de não escorregamento:
Traduzindo essa equação para o português:
A velocidade do fluido na parede é igual a velocidade da parede, ou seja, a camada de fluido que está diretamente em contato com a parede não desliza, não escorrega, ela mantém a velocidade que a parede está
Passo 2
E agora, vamos analisar uma alternativa de cada vez. o/
A letra (A) fala sobre fluidos ideais, ou seja, fluidos com:
- propriedades uniformes (homogêneas)
- incompressíveis (massa específica constante)
- invíscidos (viscosidade desprezível)
Um fluido invíscido possui viscosidade aproximadamente zero.
Como a viscosidade é uma propriedade relacionada à resistência do fluido ao escoamento, quando , então quase não há resistência para escoar.
Com isso, mesmo que a parede esteja parada, o fluido vai conseguir escoar com sua própria velocidade, porque o atrito será quase nulo. Ou seja, a camada de fluido em contato com a parede vai ter uma velocidade diferente em relação a ela. Conclusão: fluidos ideais deslizam

Logo, fluidos ideais não satisfazem a condição de não deslizamento. Descartamos a alternativa (A).
A alternativa (B) fala de fluidos compressíveis:
Nos fluidos compressíveis, a massa específica varia. Como vimos na alternativa (A), a característica que influencia na velocidade do escoamento é a viscosidade, pois ela está relacionada à resistência ao escoamento (ao atrito!)
A massa específica variar diz respeito a massa e volume ocupado pelo fluido, o que não altera a velocidade do fluido na parede. Então, eliminamos a alternativa (B).
Estamos chegando lá! E os fluidos não newtonianos da letra (C)?
Os fluidos não newtonianos não seguem a Lei de Newton da Viscosidade, ou seja:
Isso significa que em fluidos não newtonianos a tensão cisalhante não é diretamente proporcional à taxa de deformação . Então, nesse tipo de fluido, a viscosidade pode variar.
Além disso, fluidos não newtonianos podem ser compressíveis ou incompressíveis, viscosos ou não viscosos. Então, não podemos afirmar que a condição de não escorregamento é válida para todo fluido não newtoniano. Por isso, a resposta não é a letra C.
Finalmente, chegamos na letra D! Por eliminação sabemos que ela está certa. Mas por que a condição de não-deslizamento é válida para todos os fluidos viscosos?
Isso acontece pois fluidos viscosos possuem , ou seja, há resistência ao escoamento, temos atrito. Por conta dessa resistência, a camada de fluido mais próxima à parede vai ficar com a mesma velocidade da parede.
Como está acontecendo um escoamento, vamos ter uma distribuição de velocidade, em que as camadas acima desta ficam com velocidades maiores, até atingir um valor máximo. Se tiver outra parede em cima, a distribuição de velocidade seria algo parecido com isso:

Então, a condição de não escorregamento é válida para todo fluido viscoso.
Resposta
Alternativa (D) Viscosos
Exercício Resolvido #2
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 289, ex. P 4.43
Para o filme líquido (viscoso) de espessura constante sendo drenado na figura a seguir, quais são as condições de contorno apropriadas (a) no fundo em y = 0 e (b) na superfície em y = h?
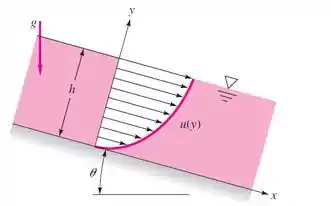
Passo 1
Esse exercício nos pede as condições de contorno. Analisando o fundo desse escoamento, ou seja, onde y = 0, temos uma parede, certo?
Isso significa que temos uma condição de fronteira. Assim, podemos aplicar em , a condição de não deslizamento, ou a hipótese de não-escorregamento
Nesse exercício, a velocidade é , logo
Como a parede está parada (no enunciado não há nada informando se a superfície está em movimento), então a velocidade do fluido naquele ponto será zero
Então, a condição de contorno no fundo é
Passo 2
Agora vamos analisar a superfície superior do escoamento, ou seja, onde y = h
Nessa parte não há uma parede. Então não podemos aplicar a condição de não deslizamento. Porém, se não há parede (placa ou barreira), não há tensão cisalhante
Considerando que o fluido é newtoniano, ele obedece a Lei de Newton da Viscosidade
A tensão cisalhante é 0 em y = h, logo
No fluido newtoniano, a viscosidade é constante, então:
E essa é a condição de contorno na superfície em y = h.
Resposta
a)
b)
Exercício Resolvido #3
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 289-290, ex. P 4.44
Vamos analisar a expansão brusca do escoamento no tubo da figura, usando as equações completas da continuidade e de Navier-Stokes. Quais são as condições de contorno apropriadas para lidar com esse problema?
Obs: Quando o escoamento em um tubo se alarga bruscamente, como na figura, aparecem turbilhões de baixa velocidade e baixo atrito nos cantos, e o escoamento gradualmente se alarga até A2 a jusante.
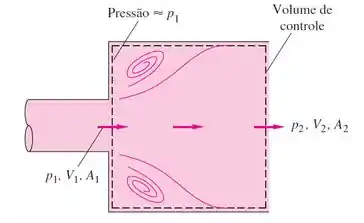
Passo 1
Opa! Para encontrar as condições de contorno, vamos por partes. Nesse exercício, temos:
- condições de fronteira (paredes)
- condições de entrada/saída (velocidade)
- condições de entrada/saída (pressão)
Com essas condições, conseguimos utilizar e simplificar as equações da continuidade e Navier-Stokes.
Como são tubos, vamos adotar a coordenada r para o raio e z para a direção do escoamento, ok? Então vamos lá, começando pelas condições de fronteira.
Todas as paredes são fronteiras. E como o enunciado não menciona que esse tubo está em movimento, então vamos considerar que ele está parado (velocidade = 0).
Logo, pela condição de não-escorregamento, a velocidade do fluido nas paredes é zero
As paredes correspondem a , , além da superfície vertical onde ocorre o aumento brusco de raio. Logo, as velocidades e nesses pontos são nulas
Essas são as condições de contorno de fronteira
Passo 2
Para as condições de contorno de entrada (1), devemos considerar que a distribuição de velocidades é conhecida na primeira parte da tubulação a partir de um certo
Além disso, na saída (2) precisamos conhecer também o comportamento da velocidade. Isso acontece a partir de , após os turbilhões de velocidade se estabilizarem.
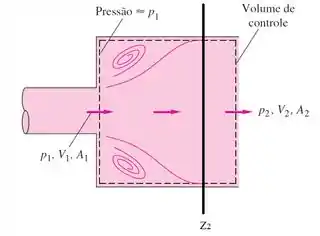
Finalmente, precisamos definir como condição de contorno a entrada ou a saída da pressão. Assim, utilizando a equação da Continuidade e Navier-Stokes será possível calcular a pressão na seção que se deseja conhecer (saída ou entrada)
Em geral, conhecemos a entrada dos escoamentos e queremos saber o que acontece na saída. Fazendo a hipótese de que a pressão na entrada (1) é conhecida, temos a seguinte condição válida:
E assim encontramos todas as condições de contorno para aplicar a continuidade e Navier-Stokes nesse problema. 😊
Resposta
Condições de fronteira (parede):
Condições de entrada/saída:
Exercício Resolvido #4
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 290, ex. P 4.45
Vamos analisar o escoamento oscilatório no tubo U da figura usando as equações completas da continuidade e de Navier-Stokes. Quais são as condições de contorno adequadas para resolver este problema?
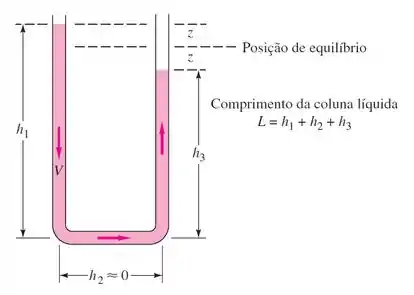
Passo 1
Temos um escoamento oscilatório... o que isso significa?
Significa que nesse tubo em U existe uma situação inicial e outra final, e a coluna de líquido oscila para chegar na posição de equilíbrio. Então o escoamento nesse exercício não é permanente: o regime é transiente.
Ok! Então quais seriam as condições de contorno?
Como nosso regime é transiente, isto é, as propriedades variam com o tempo, nós precisamos conhecer as condições iniciais. Precisamos responder à pergunta: Em quais alturas z estão cada lado da coluna de líquido em t = 0?
Posicionando a referência
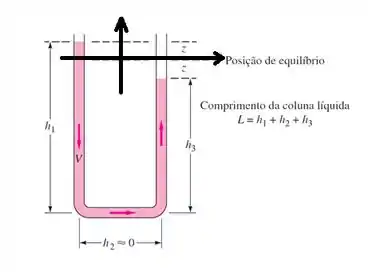
Além disso, vamos assumir que o sistema está inicialmente parado como condição inicial também
Passo 2
Até aqui definimos as condições iniciais do problema. Agora precisamos definir as condições de fronteira. Nesse problema temos 2 tipos de condições de fronteira
- Paredes (o tubo em U é uma barreira sólida ao escoamento)
- Interfaces (a coluna de líquido tem 2 interfaces com a atmosfera)
Nas paredes, onde o raio é o raio do tubo (r=R), pela condição de não deslizamento, a velocidade do fluido será zero
Além disso, na interface temos um sistema fluido/atmosfera. Considerando que a variação de altura da coluna não é brusca, a pressão do fluido é a pressão atmosférica nos pontos de interface
Com essas condições, conseguimos resolver o problema :D
Resposta
Condições iniciais
Condições de fronteira
Exercício Resolvido #5
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 290, ex. P 4.46
Fluido de um grande reservatório à temperatura escoa por um tubo circular de raio R. As paredes do tubo estão envolvidas por uma resistência elétrica que fornece calor para o fluido a uma taxa (energia por unidade de área da parede). Se quisermos analisar este problema usando as equações completas da continuidade, de Navier-Stokes e da energia, quais são as condições de contorno apropriadas para a análise?
Passo 1
Oi! Nesse exercício, vamos pensar nas condições de contorno não só para a continuidade e Navier-Stokes (o que envolve velocidade e pressão), como também para a equação da energia, o que envolve temperatura.
As nossas condições de contorno são:
- condições de entrada (z = 0)
- condições de fronteira (parede)
Condições de entrada
A situação mais comum nesse tipo de problema é considerar que o perfil de velocidade na entrada do tubo é conhecido, uniforme e puramente axial (componente radial da velocidade é nula). A velocidade é descrita por

Do mesmo modo, podemos considerar a temperatura na entrada (z = 0) uniforme e igual a uma constante
Além disso, para resolver Navier-Stokes, a pressão na entrada também pode ser conhecida
Beleza, conhecemos as condições de entrada!
Passo 2
Na parede, vamos considerar a condição de não deslizamento
A parede é onde r = R e ela está parada, então
Além disso, assumimos que o escoamento ocorre apenas na direção z (puramente axial)
Para fechar, a cereja do bolo sobre a fronteira é essa parte do enunciado:
“As paredes do tubo estão envolvidas por uma resistência elétrica que fornece calor para o fluido a uma taxa (energia por unidade de área da parede)”
Essa taxa pode ser definida dessa forma (considerando que o calor entrando no sistema é positivo):
Será que essas unidades estão certas? Vamos conferir
Confere! Então, essa equação é válida na parede, ou seja, em r = R
Agora sim, cereja do bolo colocada, encontramos as condições de contorno no problema. o/
Resposta
Condições de entrada
Condições de fronteira (parede)
Exercício Resolvido #6
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 289, ex. P 4.36
Um filme de espessura constante de um líquido viscoso flui em movimento laminar descendo por uma placa inclinada a um ângulo , como na Figura. O perfil de velocidade é:
Encontre a constante em termos do peso específico e da viscosidade e do ângulo . Encontre a vazão volumétrica por unidade de largura em termos desses parâmetros.
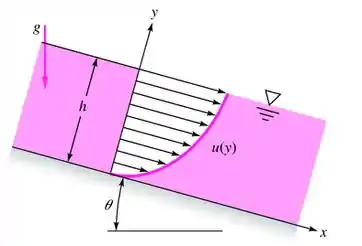
Passo 1
Fala galera! Então esse exercício envolve um pouquinho de Equação da Continuidade, um pouco de Navier-Stokes e no final vamos aplicar as condições de contorno que o problema nos fornece.
Temos as seguintes informações de contorno:
Líquidos são normalmente incompressíveis e apresentam viscosidade constante:
Passo 2
Vamos checar para ver se a continuidade é satisfeita nesse escoamento:
Aplicando nosso campo de velocidades:
Sobra o seguinte termo
Que também é zero, logo o escoamento satisfaz a continuidade.
Passo 3
Como a massa específica e a viscosidade são constantes, podemos utilizar as esquações de Navier-Stokes:
Sabemos que depende apenas de e que
Se decompormos a força gravitacional nas componentes fornecidadas:
Substituindo na primeira expressão o valor de e :
Se , em qualquer a pressão é constante. Logo:
Ou em função do peso específico
Passo 4
Sabemos de quando calculávamos vazão que:
No nosso caso calcularemos a vazão por unidade de largura, que no caso é
Se
Substituindo
Resposta
Letra a)
Letra b)
Exercício Resolvido #7
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 266, ex. 5.9
(Adaptada) Um líquido escoa para baixo sobre uma superfície plana inclinada em um filme laminar, permanente, completamente desenvolvido e de espessura . Considerando as equações da continuidade e Navier-Stokes simplificadas abaixo, obtenha expressões para o perfil de velocidades do líquido, a distribuição de tensões de cisalhamento, a vazão volumétrica e velocidade média. Relacione a espessura do filme de líquido com a vazão volumétrica por unidade de água com espessura , escoando sobre uma superfície de largura , inclinada de em relação à horizontal.
Equação da continuidade simplificada
Equação de Navier-Stokes simplificada
Passo 1
UAU! Esse exercício pediu coisa para caramba, mas nem deu tanta informação assim! Quem poderá nos defender?

Primeiro, vamos ilustrar o que está acontecendo:
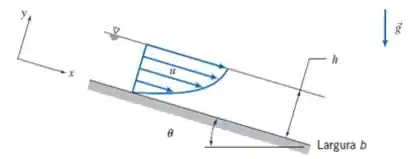
Temos duas condições de contorno. Uma delas é a condição de não deslizamento. Na placa, ou seja em y = 0, a velocidade u do fluido é 0, pois a placa está parada.
A outra está relacionada a superfície livre, ou seja, na superfície do fluido mais distante da placa (y=h). Já que não há um sólido ali para que seja possível aplicar uma força paralela ao movimento, podemos considerar que a tensão de cisalhamento ali é zero!
Lembrando que a água é um fluido newtoniano, vale a Lei de Newton da Viscosidade
Logo, a taxa de deformação du/dy será zero em y = h
Essas são as condições de contorno que vão nos ajudar a resolver a questão. Vamos voltar para as equações então?
Passo 2
As equações de Navier-Stokes simplificadas para esse caso foram dadas no enunciado e são essas aqui:
Para descobrir o perfil de velocidade que o enunciado pediu, vamos integrar a primeira equação, beleza? Vamos isolar o termo no qual a velocidade u aparece!
Daí, pela geometria do problema, a componente da gravidade na direção x é:
Substituindo em Navier-Stokes
Agora sim, hora de integrar. No lado direito, nenhuma variável depende de y 😉
Precisamos integrar mais uma vez
Passo 3
Para descobrir e , vamos aplicar as condições do contorno no Passo 1. A primeira foi a condição de não deslizamento:
Aplicando no perfil de velocidade
Atualizando o perfil de velocidade:
A segunda condição de contorno foi da tensão cisalhante na superfície livre (y=h)
A expressão de du/dy é
Em y=h:
Logo
Atualizando o perfil de velocidades
Colocando em evidência
Show! Encontramos o perfil de velocidades usando as condições de contorno! Com ele dá para achar a expressão da tensão cisalhante
Passo 4
Para achar a distribuição de tensão de cisalhamento, vamos usar a Lei de Newton da Viscosidade
No passo anterior descobrimos u, logo du/dy é:
Substituindo na Lei de Newton da Viscosidade:
E essa é a distribuição de tensão cisalhante
Passo 5
Agora é a vez da vazão volumétrica. Vamos usar a definição de vazão:
A área é a área transversal do escoamento. É uma largura b (entrando na tela) multiplicada pela altura y
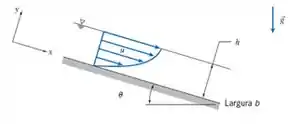
Sabemos que u é o perfil de velocidade
Integrando
Essa é a vazão volumétrica :D Suuucesso! Agora, vamos calcular a velocidade média.
Passo 6
Sei que é muita coisa, mas a velocidade média já tá quase toda calculada. Ela é vazão volumétrica sobre área transversal
Acabamos de calcular Q, vamos substituir
Simplificando
Viu! Rapidinho achamos :D
Passo 7
Finalmente, vamos lembrar da última parte do enunciado
“Relacione a espessura do filme de líquido com a vazão volumétrica em um filme de água com espessura , escoando sobre uma superfície de largura , inclinada de em relação à horizontal.”
Traduzindo: encontre a vazão volumétrica utilizando esses números indicados na figura
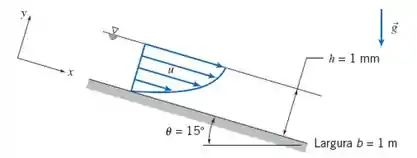
Lembrando que já calculamos a expressão da vazão volumétrica
Substituindo
Como o fluido é a água
YAY! Fechamos o exercício 😉 Foi longo, mas olha quanta coisa conseguimos achar utilizando as condições de contorno em Navier-Stokes!
Resposta
Perfil de velocidade
Distribuição de tensões de cisalhamento
Expressão de vazão volumétrica
Velocidade média
Vazão volumétrica para
Exercício Resolvido #8
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 269, ex. 5.10
(Adaptada) Um líquido viscoso enche o espaço anular entre dois cilindros concêntricos verticais. O cilindro interno é estacionário e o cilindro externo gira com velocidade constante. O escoamento é laminar. A equação simplificada de Navier-Stokes está indicada abaixo. Obtenha expressões para o perfil de velocidades do líquido.
Equação da Navier-Stokes simplificada
Passo 1
Vamos começar entendendo melhor esse espaço anular? Essa figura ilustra o escoamento:
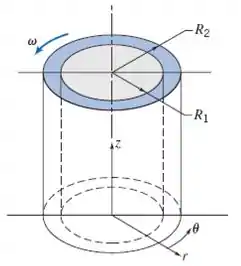
Os cilindros são concêntricos, sendo que o de dentro está parado e o de fora está girando. Com isso, temos as condições de contorno!
Afinal, qual delas? Iremos aplicar nos cilindros a condição de não-deslizamento, beleza? Vamos lá
No cilindro interno, ou seja, em , pela condição de não-deslizamento, o fluido estará parado, pois o cilindro de dentro está parado. Logo,
Olhando para o cilindro externo, ou seja, em r = , por essa mesma condição (a de não deslizamento), a velocidade do fluido será...
Dessa vez, a velocidade não é zero, pois o cilindro de fora está se movendo. Ele se move justamente com essa velocidade 😊
Beleza! Agora que sabemos as condições de contorno, vamos dar uma olhadinha na equação que o enunciado deu.
Passo 2
A equação de Navier-Stokes simplificada é
Como queremos encontrar o perfil de velocidades, precisamos integrar essa equação.
Integrando
Integrando de novo:
Isolando , já que queremos saber o perfil de velocidades
Opa! Vamos descobrir essas constantes e agora!
Passo 3
Para descobrir essas constantes, vamos usar as condições de contorno. No cilindro de dentro, temos a condição de contorno
Substituindo no perfil de velocidade
Arrumando
Ok! Encontramos uma expressão relacionando as duas constantes c1 e c2. Vamos em busca de outra expressão através da segunda condição de contorno (a do cilindro externo)
Substituindo no perfil de velocidade
Isolando
Yes! Encontramos duas expressões descrevendo em função de . Igualando as duas expressões
Isolando :
Substituindo em uma equação de c1
Finalmente, substituindo no perfil de velocidade:
Arrumando a casa:
Encontramos o perfil de velocidade!
Resposta
Perfil de velocidade