Função Corrente e Função Potencial
Produzido por Raphael EloiTeoria
Função Corrente
Cara, você já deve ter visto as famosas equações de Navier-Stokes e da continuidade. Você viu que é um sistema enorme de EDP’s envolvendo várias funções, ou seja, é uma coisa bem complicada de resolver no braço.
Para evitar esse problema, os matemáticos meteram a cara nos livros para descobrir uma forma de reduzir o número de equações e funções para 1. Para a nossa sorte, eles conseguiram.
Primeiro eles estudaram o caso dos problemas incompressível, bidimensionais e permanentes, ou seja, nada depende do tempo. Matematicamente falando, a equação da continuidade se reduz a:
Agora, a ideia de 1 milhão de dólares foi: imaginar uma função mágica que sempre satisfaz essa equação, porque dai a gente poderia se livrar dela. Eis que surge a famosa função corrente. Ela é denotada por e é definida desse jeitinho aqui:
Olha o que ocorre ao introduzirmos essa mudança na equação da continuidade
Portanto, a equação da continuidade é sempre satisfeita e podemos desprezar essa equação já que ela não traz nenhuma novidade sobre o escoamento. É assim que definiremos a função corrente nos outros sistemas de coordenadas, acharemos a função que sempre satisfaz a continuidade.
Duas coisas interessantes sobre a função corrente são: se fizermos igual a uma constante o resultado será uma linha de corrente. Por exemplo, se tivermos
A gente vai fazendo e isso vai nos dando curvas que são as linhas de corrente representadas abaixo:
O outro fato maneiro é que ela mede a vazão volumétrica entre duas linhas de corrente 1 e 2, através da seguinte fórmula
Então se o escoamento vai para a direita e caso contrário vai para a esquerda, beleza?
Vorticidade e Irrotacionalidade
Nessa vibe de definir funções matemáticas para escoamentos, os matemáticos foram além e definiram uma função chamada vorticidade. Ela é representada pela letra e definida desse jeitinho aqui:
Ou seja, ela é calculada como o rotacional do campo de velocidades! Repara que ela é um vetor!
Ela é importante, porque a velocidade angular do fluido, , é definida como metade da vorticidade. Em termos matemáticos é isso aqui
Para acabar as definições, existe um termo que aparece com frequência nas provas que é o escoamento irrotacional. Cara, quando ele diz isso, ele está nos contando que , ou seja, a vorticidade e a velocidade angular são ambas nulas.
A maior parte dos escoamentos é irrotacional. Então, quando teremos o rotacional diferente de zero? Em alguns casos, mas basicamente quando tivermos em regiões onde os efeitos viscosos são importantes tipo na camada limite!
Função Potencial
Vimos que a função corrente facilita a analise de escoamentos bidimensionais. Po, e os escoamentos tridimensionais? Não podemos fazer nada?
Os matemágicos perceberam que se o escoamento for irrotacional, a gente pode achar uma função chamada função potencial que é definida desse jeito aqui
Ou seja, temos o seguinte
Com essa função mágica, podemos reduzir o problema de 3 funções para apenas 1 a função potencial!
Lembra que se fizermos a função corrente igual a uma constante a gente tem linhas de corrente? Então, se fizermos a função potencial igual a uma constante a gente tem linhas ou superfícies equipotenciais.
Um último fato interessante desses carinhas é que as linhas de corrente são sempre ortogonais as linhas ou superfícies equipotenciais.
São várias funções novas e conceitos diferentões, eu sei. Mas, vai lá nos nossos exercícios praticar um pouco que você vai ver que vai ficar tudo bem mais claro.
Vorticidade e Irrotacionalidade
Função Potencial
Exercícios Resolvidos
Exercício Resolvido #1
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um escoamento incompressível bidimensional é dado pelo campo de velocidade , em unidades arbitrárias. Esse escoamento satisfaz a continuidade? Em caso afirmativo, encontre a função corrente e faça um gráfico de algumas linhas de corrente, com setas.
Passo 1
Como ele já nos deu o campo de velocidades, a gente tem que
Passo 2
Para ver se esse escoamento satisfaz a equação da continuidade, devemos ver se satisfazem a seguinte equação
Passo 3
Pelas expressões do passo 1, temos que
Então temos que
Logo o escoamento satisfaz a equação da continuidade
Passo 4
A definição da função corrente é
Então temos que seguir o passo a passo abaixo
Passo 5
Escolha uma das duas equações para integrar
Por conveniência, vou integrar a equação do , ou seja
Essa função surgiu porque qualquer coisa que dependesse só de foi tratada como constante ao fazer a derivada parcial com respeito a .
Passo 6
Derivamos a expressão obtida no passo anterior com relação a outra variável, ou seja, devemos calcular:
Fazendo as continhas, temos
Passo 7
Pela definição da função corrente, temos que
Integrando a equação acima, temos
Passo 8
Assim, juntando tudo temos que
Passo 9
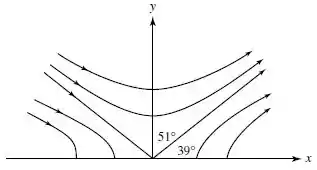
Colocando os valores de , temos hipérboles como na figura abaixo!
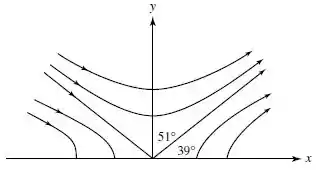
Resposta
Satisfaz a equação da continuidade!
Exercício Resolvido #2
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Considere o seguinte escoamento incompressível bidimensional, que claramente satisfaz a continuidade:
Encontre a função corrente para esse escoamento usando coordenadas polares.
Passo 1
A função corrente é definida em coordenadas cartesianas como:
Depois que acharmos a expressão de , mudamos as coordenadas com mudanças polares abaixo
Passo 2
Seguindo o passo a passo, devemos escolher uma das duas equações do passo 1 para integrar. Vamos escolher a primeira:
Passo 3
Agora, derivamos a expressão obtida no passo anterior com relação a outra variável que aqui é , ou seja, calculamos
Calculando, temos
Passo 4
Usando a definição de função corrente, temos
Passo 5
Juntando tudo, temos que
Passo 6
Para passar para coordenadas polares, basta fazer a mudança polar enunciada no passo 1.
Resposta
Exercício Resolvido #3
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Para a distribuição de velocidades a seguir, determine se existe uma função corrente e, se existir, encontre uma expressão para e faça o esboço da linha de corrente que passa pelo ponto .
Passo 1
A função corrente é definida em coordenadas cartesianas como:
Devemos aplicar o passo a passo
Passo 2
Seguindo o passo a passo, devemos escolher uma das duas equações do passo 1 para integrar. Vamos escolher a segunda:
Passo 3
Agora, derivamos a expressão obtida no passo anterior com relação a outra variável que aqui é , ou seja, calculamos
Calculando, temos
Passo 4
Usando a definição de função corrente, temos
Passo 5
Juntando tudo, temos que
Passo 6
Substituindo o ponto na equação acima, temos que
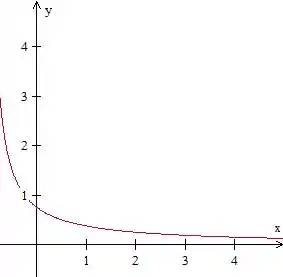
Assim, devemos plotar a seguinte curva
O que gera a imagem abaixo
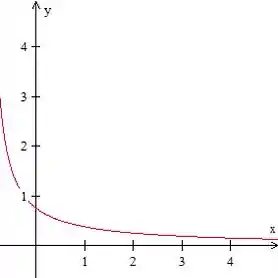
Resposta
Exercício Resolvido #4
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um campo de escoamento incompressível bidimensional é definido pelos componentes de velocidade
em que e são constantes. Se elas existem, encontre a função corrente e o potencial de velocidade.
Passo 1
Para verificar se existe a função corrente, devemos ver se o escoamento atende a equação da continuidade, ou seja, se:
Para ver se existe o potencial de velocidade, devemos ver se o escoamento é irrotacional, ou seja, se:
Passo 2
Comecemos com a função corrente. Temos que
Assim, a equação da continuidade é satisfeita, pois
Então a função corrente existe e vamos seguir o passo a passo para descobri-la.
Passo 3
Vamos escolher a primeira equação para integrar. Temos, então
Passo 4
Agora devemos derivar o obtido no passo acima com relação a outra variável, ou seja, :
Passo 5
Pela definição de função corrente, temos que:
E, pelo enunciado:
Então:
Passo 6
Juntando tudo, temos que
Passo 7
Agora, vamos ver se o potencial existe, ou seja, ver se o escoamento é irrotacional. Em vez de usar a notação com matriz, sempre que tivermos um campo com duas componentes, podemos usar essa notação simplificada para o rotacional:
Fazendo nossas continhas, temos que
Assim, não há potencial para a velocidade!
Resposta
Exercício Resolvido #5
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Considere o potencial de velocidade incompressível bidimensional . É verdade que , e, em caso afirmativo, o que isso significa? Se ela existe, encontre a função corrente desse escoamento. Encontre a equação da linha de corrente que passa por .
Passo 1
a) O Laplaciano, , é definido da seguinte forma
Então, devemos calcular essas derivadas e ver se isso dá zero.
Passo 2
Calculando, temos
Assim o Laplaciano é
Passo 3
A equação da continuidade incompressível, escrita numa notação vetorial, é dada por
A definição do potencial de velocidade é
Colocando uma equação dentro da outra e lembrando que , temos
Ou seja, sempre que o Laplaciano é zero a equação da continuidade incompressível é satisfeita.
Passo 4
b) Para determinar a função corrente, devemos descobrir as componentes do vetor velocidade. Para isso usamos a definição de potencial de velocidade, ou seja
Depois, aplicamos o passo a passo que vimos nos outros exercícios.
Passo 5
Derivando a expressão de , temos que
Agora vamos integrar a seguinte equação
Passo 6
Derivando a expressão do passo anterior com relação a , temos
Pela definição da função corrente, temos
Passo 7
Juntando tudo, temos que
Passo 8
c)Substituindo o ponto na função obtida acima, temos que
Assim, a curva que passa pelo ponto é
Resposta
Exercício Resolvido #6
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
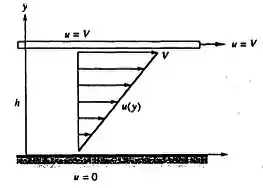
Mostre que o escoamento de Couette linear entre placas na Figura tem uma função corrente, mas não tem potencial de velocidade. Qual é a razão disso?
Passo 1
A primeira coisa que temos que achar são as componentes do vetor velocidade. A componente é simples de achar, porque o próprio desenho nos mostra
A componente varia linearmente, lá no gráfico o perfil é uma reta, de 0 na posição até na posição , então pela equação da reta a gente tem que
Passo 2
Para saber se existe função corrente, temos que ver se a equação da continuidade é satisfeita, então vamos lá
Então ,temos que
Logo, o escoamento satisfaz a equação da continuidade e a função corrente existe.
Passo 3
Para descobrir qual é a função corrente a gente segue o mesmo passo a passo, vamos integrar a expressão de primeiro:
Derivando com relação a a expressão de que a gente acabou de achar, temos
Comparando com a componente , temos
Logo, a função corrente é da forma
Passo 4
Para verificar se a função potencial existe, devemos ver se o escoamento é irrotacional. Como o escoamento tem apenas duas componentes de velocidade a gente tem que verificar essa igualdade aqui:
Passo 5
Fazendo as contas a gente tem que
Assim, a gente tem que
Logo o escoamento é rotacional e não admite função potencial!
Resposta
Não existe função potencial!
Exercício Resolvido #7
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Encontre o potencial de velocidade bidimensional para o padrão de escoamento em coordenadas polares , , em que e são constantes.
Passo 1
Cara, vou te contar um segredo que você tem que guardar no seu coração: em coordenadas polares a expressão da função potencial fica assim:
Ou seja, nesse exercício a gente precisa achar a bendita que satisfaz essas igualdades.
Passo 2
Vou começar olhando para (você poderia ter começado por se preferir):
Passo 3
Agora a gente tem que achar quem é essa tal de . Para isso, usamos a outra equação, ou seja
Passo 4
Agora é só juntar tudinho e vamos ficar com
Resposta
Exercício Resolvido #8
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Uma função corrente para um escoamento plano, irrotacional em coordenadas polares é:
Onde são constantes. Encontre o potencial de velocidade para esse escoamento.
Passo 1
Essa daqui vai misturar os conceitos todos, então temos que acompanhar com bastante atenção! Como ele disse que o escoamento é irrotacional, a gente sabe que o potencial existe! Mas, para encontrar sua carinha a gente precisa das componentes da velocidade então é isso que vamos fazer primeiro, usando as equações
Essas são as equações da função corrente em coordenadas polares!
Passo 2
A gente tem que
Então, pelas equações do passo 1, temos que
Passo 3
Com as componentes em mãos, podemos calcular o potencial com essas equações
Passo 4
Vou começar analisando a primeira equação:
Integrando dos dois lados com relação a a gente tem que
Passo 5
Agora derivando essa expressão de que acabamos de achar com relação a , temos que
Pela expressão de , temos que
Integrando a última equação, temos que
Passo 6
Juntando tudo, a gente fica com
Resposta
Exercício Resolvido #9
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
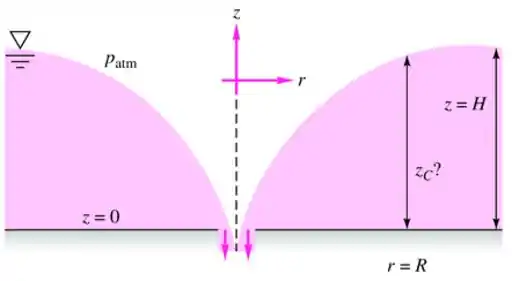
Um líquido é drenado por um pequeno furo em um tanque, como mostra a Figura, de forma que o campo de velocidade é dado por , , , em que é a profundidade da água distante do furo. Esse padrão de escoamento é rotacional ou irrotacional? Encontre a profundidade da água no raio .
Passo 1
Primeiro temos que ver se o escoamento é irrotacional. Vou te dar outra expressão que vai facilitar a sua vida quando tiver trabalhando com coordenadas polares! Para ver se um escoamento em coordenadas polares é irrotacional, a gente tem que verificar essa equação:
Passo 2
Pelo enunciado a gente sabe que
Como é uma constante, o primeiro termo da equação do passo 1 é zero. Como não depende de o segundo termo da equação também é zero, logo o escoamento é irrotacional.
Passo 3
Cara, quando a gente vê esses exercícios com altura e pressão a gente fica com uma vontade de tacar Bernoulli né não?
Então, a gente tem que tomar cuidado, porque a gente só pode fazer isso com uma série de hipóteses sendo satisfeitas e numa mesma linha de corrente.
Sabe uma parte ótima dos escoamentos irrotacionais? A equação de Bernoulli é válida sempre nesses escoamentos!
Show, então podemos escrever o seguinte:
Passo 4
Agora, precisamos entender que são alguns desses termos aí! Pô, a única componente do vetor velocidade que não é nula é , então o módulo da velocidade é igual a essa componente. Assim,
Fazendo o limite quando a gente acha o termo que é
Passo 5
Substituindo esses valores na equação de Bernoulli, a gente acha que
Resposta
O escoamento é irrotacional