Método dos Parâmetros Concentrados
Teoria
Introdução
A gente já estudou muitas coisas, mas todas tinham algo em comum: a gente sempre assumia que o estado era estacionário. Sendo assim, as propriedades não mudavam ao longo do tempo.
Mas imagina que você pegue um corpo que está dentro do forno a uma temperatura alta e a coloque em uma piscina com água bem gelada . Se a gente acompanhar a temperatura desse corpo, ela vai diminuir ao longo do tempo.
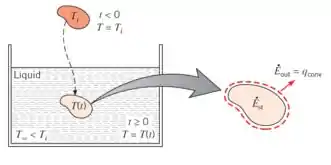
Logo que a gente coloca o corpo ali dentro, existe um gradiente de temperatura entre ele e o fluido, gerando um fluxo de calor. Sendo assim, o corpo perde energia. Ao perder essa energia, sua temperatura diminui. E isso acontece até a temperatura do corpo se igualar à do fluido.
Esse é um caso típico de um problema em que uma propriedade (a temperatura) varia no tempo. A isso chamamos de regime transiente!
No caso do regime estacionário, a gente conseguiu várias expressões analíticas para descrever o perfil de temperatura na parede plana, na esfera, no cilindro... Mas com o regime transiente não é tão fácil, as soluções analíticas são bem mais raras!
Mas o que é o método dos parâmetros concentrados?
Pois bem, o método dos parâmetros concentrados é uma das poucas soluções analíticas que a gente pode conseguir. Mas, como nada é de graça, pra usar esse método a gente adota uma simplificação:
“A condutividade do material () deve ser considerada infinita, para que a temperatura do sólido seja constante a cada instante de tempo.”
Não existem materiais com condutividade térmica () infinita. Mas, se a resistência de condução no interior do sólido for muito pequena quando comparada a resistência de convecção , aí a gente pode assumir que a condutividade térmica é “infinita”. Ou seja:
Dividindo os dois lados da inequação por , a gente fica com:
Para o caso da parede plana, a gente pode substituir as expressões das resistências:
Reorganizando a inequação:
Pronto! Agora tá mais tranquilo de ver como a gente define, na prática, se essa aproximação é válida. Com os valores de , e conhecidos, a gente calcula essa razão e verifica se o valor é muito menor do que .
Só que essa razão é tão importante que recebe uma nomenclatura especial, esse é o que chamamos do número de Biot ():
Mas você pode estar pensando: “Se esse número der já tá bom? Ou ele tem que ser pra eu considerar que é muito menor do que ?”
É uma ótima pergunta! Muitos experimentos foram feitos e observaram que a simplificação já é válida se:
Então, se der você não pode usar esse método dos parâmetros concentrados, mas se der já pode!
A gente só vai usar esse método pra parede plana?
Ótima pergunta, pequeno gafanhoto! E a resposta é “não”! A gente pode usar pra esferas e cilindros também usando o mesmo cálculo do número de Biot ().
Só que o comprimento vai virar um comprimento característico e ele pode ser definido de duas formas:
- Razão entre o volume e a área superficial do sólido.
- Comprimento correspondente à maior diferença de temperatura no sólido.
Pra calcular pela primeira definição, basta saber como calcular os volumes e áreas, mas pra usar a segunda definição, você tem que prever onde seria o ponto mais quente e onde seria o ponto mais frio no sólido e encontrar essa distância.
Mas fica tranquilo, que eu já coloquei tudo bonitinho aqui pra você! Dá uma olhada:
Tudo muito bonito, mas como fazer os exercícios?
Isso aí! Pra isso, nada melhor que um exemplo! Você se lembra daquele corpo tava quente () e você imergiu num fluido frio (). Bora falar dele então!
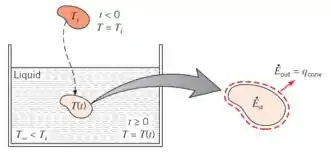
Como tudo em Transferência de Calor, bora fazer um balanço de energia nesse corpo:
Como não tem nenhuma energia entrando e o corpo não gera calor por si só, a gente fica com:
A taxa de calor de saída () é uma taxa de convecção, então a gente sabe como escrever sua expressão. E a taxa de acúmulo () a gente já viu como pode escrever também:
Em que é a temperatura do corpo num dado instante e vale no início ().
Vamos fazer aquela mudança de variável para a temperatura de excesso ():
Essa é a equação que a gente tem pra resolver! Existem basicamente dois casos de problemas envolvendo o regime transiente:
Caso A: A gente sabe qual a temperatura final do corpo e queremos saber quanto tempo é necessário pra que essa temperatura seja alcançada. (Variável de interesse: )
Caso B: A gente sabe quanto tempo o corpo vai ficar exposto ao fluido e quer saber sua temperatura final. (Variável de interesse: )
Então a gente pode resolver a equação de duas maneiras, uma para cada caso:
Caso A: Solução para o tempo.
Integrando em ambos os lados:
Caso B: Solução para a temperatura.
Aplicando a exponencial em ambos os lados e isolando o termo , a gente fica com:
Podemos escrever mais suscintamente a expressão como:
Em que, a constante de tempo () é dada por:
OBS: Nessa solução, a gente pode ainda reorganizar os termos dentro do expoente e verificar a presença de dois números adimensionais importantes: o número de Biot () e o número de Fourier ().
Em que:
Como calcular a quantidade de calor trocada?
Além de saber a temperatura ou o tempo, às vezes a gente tá interessado em saber a quantidade de energia total que foi transferida (). Pra isso, basta a gente integrar a taxa de calor ao longo do tempo:
Substituindo a expressão da temperatura de excesso que encontramos:
Integrando a expressão:
Prontinho! Agora você já tá preparado pra enfrentar os desafios do regime transiente com o método da capacidade concentrada!
A gente só vai usar esse método pra parede plana?
Tudo muito bonito, mas como fazer os exercícios?
Como calcular a quantidade de calor trocada?
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um armazenamento de energia térmica consiste em um grande canal retangular no qual é bem isolado em sua superfície externa e engloba camadas alternadas de material de armazenagem e canal de escoamento.
Cada camada do material de armazenamento é uma placa de alumínio () de largura , a qual está a uma temperatura de . Considere condições para as quais a unidade de armazenamento é carregada pela passagem de um gás quente através dos canais. A temperatura do gás e o coeficiente de convecção são considerados valores constantes de e em todo o canal.
Quanto tempo irá levar para atingir da energia armazenada máxima possível?
Qual será a temperatura do alumínio nesse instante?
Passo 1
Quanto tempo irá levar para atingir da energia armazenada máxima possível?
A gente pode encarar o problema como sendo várias paredes planas, tais que:
Dessa maneira, a gente precisa calcular o número de Biot do bloco pra verificar a validade da aproximação do método dos parâmetros concentrados ().
Para o caso das paredes planas, o comprimento característico () é exatamente a metade da largura da parede (), então:
Substituindo os valores:
Como , a gente pode usar o método dos parâmetros concentrados!
Passo 2
O enunciado nos pede qual é o tempo () pra que a quantidade de energia armazenada atinja da quantidade máxima de calor (). A gente pode escrever da seguinte maneira:
A gente sabe que a quantidade de calor na situação do corpo sob convecção somente depende do tempo e é dada por:
Vamos entender então o que acontece em diferentes momentos:
No instante inicial, a transferência de calor ainda não começou, logo a quantidade de calor trocado será igual a zero, como podemos ver substituindo na equação:
Daí pra frente, quanto maior o valor de , menor será o valor da exponencial e consequentemente maior será a quantidade de energia trocada. Sendo assim, o máximo de calor trocado é atingido quando o tempo tender ao infinito:
Substituindo na equação:
Assim:
Em que:
Logo:
Isso significa aproximadamente .
Passo 3
Qual será a temperatura do alumínio nesse instante?
Agora estamos num problema do caso B, em que já sabemos o tempo () e precisamos determinar a temperatura do corpo! Sendo assim, a gente tem que:
Substituindo os valores que encontramos e já sabemos do enunciado:
Logo:
E, lembrando da definição da temperatura de excesso, a temperatura da esfera nesse instante será:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma esfera sólida de aço () de de diâmetro é revestida com uma camada de material dielétrico de espessura e condutividade térmica . A esfera revestida está inicialmente a uma temperatura de e é subitamente resfriada em um grande banho de óleo, o qual se encontra a e . Estime o tempo necessário para que a temperatura da esfera revestida atinja .
Dica: despreze o efeito do armazenamento de energia no material dielétrico, uma vez que sua capacidade térmica () é pequena quando comparada com a da esfera de aço.
Passo 1
Esse é exatamente pra gente exercitar e ver se entendemos tudo certinho! Bora lá!
A situação proposta pelo enunciado pode ser esquematizada da seguinte forma:
Bom, então a gente tem que calcular quanto tempo leva pra esfera atingir . Como é um problema transiente, a gente pode verificar se dá pra usar o método dos parâmetros concentrados
Então, bora calcular o número de Biot desse problema:
Mas aqui a gente não tem só a esfera, tem também um revestimento que a gente precisa contabilizar! Mas tem uma forma da gente simplificar isso, dá uma olhada!
A gente sabe que uma esfera aquecida sem isolamento vai perder calor para o fluido e essa transferência está associada à resistência de convecção do meio. Se colocarmos um revestimento, essa resistência à transferência aumenta e passa a ser:
Substituindo as expressões da resistência convectiva e condutiva na esfera:
Mas por que estamos fazendo isso? Porque a gente precisa de uma expressão para o coeficiente de convecção () pra calcular o , mas não podemos usar o direto, porque temos que levar em consideração a resistência do revestimento.
Agora que a gente já sabe a resistência, podemos propor um coeficiente global de transferência (), que contabiliza os dois efeitos (condução e convecção) da seguinte forma:
Dividindo pela área da esfera, a gente fica com o coeficiente global:
A gente deve calcular o com esse valor!
Passo 2
Além disso, o comprimento característico () pode ser calculado de duas maneiras:
- Razão entre o volume do sólido e a área superficial do sólido.
- Comprimento correspondente à maior diferença de temperatura no sólido.
Bora ver quanto dá cada um deles. Pela razão entre volume e área da esfera, a gente fica com:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método dos parâmetros concentrados valer ^^
Assim:
Como , a gente pode usar o método dos parâmetros concentrados! Então, vamos aos cálculos!
Passo 3
O enunciado é um exemplo do caso A, então temos que:
Podemos escrever de outra forma:
Substituindo os valores do enunciado:
Isso equivale a aproximadamente !
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Eixos de aço carbono (AISI 1010) com de diâmetro são tratados termicamente pelo aquecimento em fornalhas a gás onde os gases se encontram a e mantêm um coeficiente convectivo de .
Se os eixos entram no forno a , quanto tempo eles devem permanecer no interior da fornalha para suas linhas de centro atingirem a temperatura de ?
Dados: , , , .
Passo 1
A primeira coisa que temos que fazer aqui é calcular o número de Biot pra saber se podemos usar o Método dos Parâmetros Concentrados pra resolver o problema.
Para cilindros, de acordo com a tabela na Teoria deste tópico, , logo:
Onde:
Substituindo os valores:
Opa! Então está de boassa usar o Método dos Parâmetros Concentrados.
Passo 2
Pelo Método dos Parâmetros Concentrados nós temos que:
Agora é só reorganizar a equação pra isolar o tempo :
Onde:
Substituindo os valores:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma parede plana de um forno é fabricada de aço carbono (,, ) com espessura . A fim de proteger a parede dos efeitos da corrosão dos gases de combustão do forno, uma superfície da parede é revestida com um fino filme de cerâmica, para uma unidade de área superficial, tem uma resistência térmica de . A superfície oposta é bem isolada do ambiente.
Quando o forno entra em operação, a parede encontra-se a uma temperatura inicial de e os gases de combustão a entram no forno, promovendo um coeficiente de convecção de no filme cerâmico.
Considerando que a capacidade térmica do filme é desprezível, quanto tempo levará para a superfície interna do aço atingir a temperatura de ?
Qual é a temperatura da superfície exposta do filme cerâmico nesse instante?
Passo 1
Se a gente olhar rápido pra situação proposta acima, a gente vai achar que não dá pra usar o método dos parâmetros concentrados. Isso porque, pra usar o método, o sólido tem que estar sujeito à convecção em todos os lados.
No caso da parede plana, as duas faces devem estar sob fenômenos de convecção e, nesse exercício, nenhum dos lados tá nessa situação! Dá uma olhada:
Do lado esquerdo, a gente tem o filme cerâmico, oferecendo uma resistência adicional à transferência de calor. Mas isso a gente já viu antes! A gente pode calcular a resistência global e determinar um coeficiente global de troca térmica ().
Mas lado direito, a superfície tá isolada! Não dá pra usar essa estratégia! Pra resolver isso, a gente pode lembrar de algo que aprendemos bem lá no comecinho:
“Para resolver paredes planas com condições de contorno simétricas, basta resolver um dos lados, considerando no meio da placa fluxo zero.”
Então, a gente vai fazer ao contrário: como aqui a gente tem “metade” de uma parede plana (), a gente vai resolver como se fosse uma parede completa, porque dá no mesmo, devido à simetria!
Passo 2
Considerando que a capacidade térmica do filme é desprezível, quanto tempo levará para a superfície interna do aço atingir a temperatura de ?
A primeira coisa que temos que fazer é o que mesmo? Isso! Calcular o número de Biot:
Em que o comprimento característico () para paredes planas de comprimento é exatamente . Como estamos assumindo que a situação é metade de uma parede plana, então mesmo!
Agora o coeficiente de convecção não será o , porque temos que considerar ainda a resistência do filme cerâmico. Sendo assim, a gente precisa determinar o coeficiente global de transferência ().
A resistência total é dada por:
Como, na parede plana, o fluxo de calor é constante (já que a área é constante), a gente pode trabalhar direto com as resistências :
Substituindo a expressão da resistência convectiva:
Logo, o coeficiente global () será:
Assim o número de Biot () será:
Como , a gente pode usar o método dos parâmetros concentrados!
Passo 3
A gente precisa achar o tempo necessário para que a temperatura alcance , então esse é o caso A. Sendo assim, a gente tem que:
Substituindo os valores:
Isso equivale a aproximadamente .
Passo 4
Qual é a temperatura da superfície exposta do filme cerâmico nesse instante?
Nesse instante, a gente sabe que a temperatura da superfície interna do aço vale . A gente pode aplicar a estratégia do circuito térmico pra determinar a temperatura :
Assim:
Isolando a temperatura externa do filme cerâmico:
Substituindo os valores do enunciado:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um arame longo de diâmetro é imerso em um banho de óleo à temperatura de . O arame possui uma resistência elétrica por unidade de comprimento de . A corrente que flui através do arame vale , o coeficiente de convecção é e as propriedades do arame são ,, .
Qual é a temperatura em regime estacionário do arame?
A partir do tempo em que a corrente é aplicada, quanto tempo levará para o arame atingir uma temperatura que não exceda do valor do regime estacionário?
Passo 1
Qual é a temperatura em regime estacionário do arame?
A situação pode ser esquematizada da seguinte forma:
O item a) nos pede pra calcular a temperatura em estado estacionário, então não temos que usar ainda nenhum dos métodos de condução transiente.
A gente observa que há geração de energia térmica no corpo, devido à passagem de corrente elétrica no arame. Então, bora fazer o que a gente já tava acostumado para os casos de estado estacionário: um balanço de energia!
A taxa de calor gerada () se refere ao efeito Joule pela dissipação da energia elétrica em térmica e a taxa de saída () é dada pela convecção na superfície.
Como a resistência elétrica é dada em termos do comprimento do fio, a gente pode escrever a área também dividida pela unidade de comprimento ():
Isolando a temperatura da superfície:
Substituindo os valores do enunciado:
Passo 2
A partir do tempo em que a corrente é aplicada, quanto tempo levará para o arame atingir uma temperatura que não exceda do valor do regime estacionário?
A primeira coisa que temos que fazer é calcular o número de Biot pra saber se podemos usar o Método dos Parâmetros Concentrados:
O comprimento característico () pela razão entre volume e área do cilindro é calculado por:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método dos parâmetros concentrados valer ^^
Assim:
Como , a gente pode usar o método dos parâmetros concentrados! Então, vamos aos cálculos!
Passo 3
Esse exemplo aqui é um pouco diferente, porque tem geração de energia térmica devido à passagem de corrente elétrica no arame.
O Então, bora fazer um balanço de energia transiente nesse corpo:
OBS: Como o termo de geração não é nulo, a gente não pode utilizar aquelas equações prontas que vimos na teoria, porque elas só servem pro caso trivial de saída de calor por convecção!
Substituindo as expressões:
Isolando a derivada da temperatura no tempo:
Dividindo por “” e reorganizando:
Agora a gente pode fazer a seguinte mudança de variável:
Assim:
Integrando a equação desde o tempo inicial () até um instante qualquer:
Reorganizando:
Voltando para as variáveis convencionais (expressão para ):
Substituindo os valores do enunciado:
Aplicando o logaritmo natural na equação:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) Uma junção termopar, que pode ser aproximada como uma esfera, deve ser utilizada para a medida de temperatura em uma corrente de gás. O coeficiente de convecção entre a superfície da junção e o gás é e as propriedades termofísicas da junção são , e .
Determine o diâmetro da junção necessário para que o termopar tenha uma constante de tempo de .
Se a junção encontra-se a e é colocada em uma corrente de gás a , quanto tempo levará para que a junção alcance ?
Considere agora que também há troca de calor por radiação entre as paredes de um duto que circunda a corrente do gás. Se as paredes do duto encontram-se a e a emissividade do termopar é , calcule a temperatura do regime estacionário e determine a equação diferencial proveniente do balanço de energia transiente.
Passo 1
Determine o diâmetro da junção necessário para que o termopar tenha uma constante de tempo de .
Como a gente não sabe o valor diâmetro , a gente não consegue calcular o número de Biot, pra determinar se o Método dos Parâmetros Concentrados é válido.
Mas a gente pode tentar usar o método para encontrar esse diâmetro e depois verificar se, com esse diâmetro encontrado, o método é válido!
Sabemos que a constante de tempo () é dada por:
Sendo assim, para a esfera:
Isolando o diâmetro:
Subsituindo os valores do enunciado:
Passo 2
Agora que a gente tem o diâmetro, bora calcular o número de Biot, pra ver se é válido usar o Método dos Parâmetros Concentrados:
O comprimento característico () pela razão entre volume e área da esfera é dada por:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método dos parâmetros concentrados valer ^^
Assim:
Como , tá tudo bem a gente usar o Método dos Parâmetros Concentrados!
Passo 3
Se a junção encontra-se a e é colocada em uma corrente de gás a , quanto tempo levará para que a junção alcance ?
Agora a gente está interessado em encontrar o tempo, logo é o caso A! A gente sabe que o tempo é dado por:
Podemos escrever de outra forma:
Substituindo os valores do enunciado:
Passo 4
Considere agora que também há troca de calor por radiação entre as paredes de um duto que circunda a corrente do gás. Se as paredes do duto encontram-se a e a emissividade do termopar é , calcule a temperatura do regime estacionário e determine a equação diferencial proveniente do balanço de energia transiente.
Você poderia imaginar que esse é o caso B, mas não é! Porque tudo aquilo que vimos é para as situações que só tem convecção! E aqui a gente também tem radiação agora!
Para resolver o estado estacionário é igual ao que fazíamos nos capítulos anteriores. Pelo balanço de energia, a gente fica com:
Sendo assim, a gente fica com:
Pelos dados do enunciado:
A solução para essa equação é:
Passo 5
Considerando regime transiente, a gente fica com o seguinte balanço:
Sendo assim, a gente fica com:
Essa equação pode ser resolvida numericamente, mas esse não é nosso foco aqui!
Resposta
- A temperatura no estado estacionário vale e a equação do balanço transiente é dada abaixo:
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
A medida que as estações espaciais permanentes aumentam de tamanho, existe um consequente aumento na quantidade de potência elétrica que elas dissipam. Para manter a temperatura nos compartimentos internos dentro de limites estabelecidos, torna-se necessário transferir o calor dissipados para o espaço.
Um novo sistema proposto para a dissipação de calor é conhecido por Radiador de Gotículas Líquidas. O calor é incialmente transferido para um óleo especial para alto vácuo, que é então injetado no espaço exterior em forma de uma corrente de pequenas gotículas. A corrente percorre uma distância , ao longo da qual se resfria pela irradiação de energia para o espaço exterior, que se encontra a uma temperatura absoluta igual a zero. As gotículas são, então, coletadas e retornadas para a estação espacial.
Considere condições nas quais as gotas, com emissividade e diâmetro , são injetadas no espaço a uma temperatura e a uma velocidade .
As propriedades do óleo são , e .
Supondo que cada gota irradia calor para o espaço externo a , determine a distância necessária para que as gotículas atinjam o coletor a uma temperatura final . Qual é a quantidade de energia térmica dissipada por cada gota?
Passo 1
Vamos nessa! Logo de cara temos que calcular o número de Biot pra sabermos qual método utilizaremos pra resolver essa bagaça.
Tratando as gotículas como esferas perfeitas, o comprimento característico é dado por . Além disso, como a gotícula está perdendo calor por radiação, no lugar de , utilizaremos que é o coeficiente de transferência de calor por radiação. Dessa forma:
Onde:
Substituindo os valores:
Passo 2
Se esse fosse um problema de convecção, bastaria utilizar as equações que usamos até aqui. Mas como estamos tratando de um problema com radiação, vamos ter que voltar um pouquinho.
Se liga! Se fizermos um balanço de energia para a nossa gotícula, veremos que:
Onde , logo:
Reorganizando e integrando a equação, teremos:
Agora sim estamos prontos pra seguir em frente! :)
Passo 3
O problema nos deu que:
Substituindo os valores:
Passo 4
Já calculamos quanto tempo leva para a gotícula chegar à temperatura de , mas estamos preocupados em saber a distância que a mesma percorre até que isso aconteça.
Como as partículas foram injetadas com uma velocidade constante , podemos calcular a distância da seguinte forma:
Passo 5
Pra terminar (juro), queremos saber a quantidade de energia dissipada por cada gota.
Essa quantidade de energia é justamente a quantidade de energia que a gota perdeu para a vizinhança, logo:
Substituindo os valores:
ACABOU!
Resposta
Exercício Resolvido #8
Questão 3, UFF, P1-2017.2
Rejeitos radioativos são colocados em um recipiente esférico de parede delgada. Os rejeitos geram energia térmica por unidade de volume . O raio do recipiente é .
Assumindo que o recipiente está inicialmente a uma temperatura e sabendo que esse é colocado em um líquido inerte que se encontra a e que fornece um coeficiente convectivo uniforme.
Determine o comportamento da temperatura com o tempo no interior do recipiente.
Qual a temperatura do estado estacionário?
Determine a quantidade de calor trocada com o meio após atingir o estado estacionário.
Para todos os casos assuma modelo de parâmetros concentrados.
Expresse os resultados em termos de , , , , (condutividade térmica do rejeito), (massa específica) e (capacidade térmica do rejeito).
Passo 1
Determine o comportamento da temperatura com o tempo no interior do recipiente.
Utilizando o método dos parâmetros concentrados, fazendo o balando de energia no recipiente, teremos o seguinte:
Como não há energia entrando no recipiente:
Repare que, como temos um termo de geração de energia, não podemos usar a solução já dada pelo método dos parâmetros concentrados. Ou seja, teremos que resolver essa equação diferencial pra encontrar a temperatura em função do tempo.
Passo 2
Essa equação diferencial é separável. Assim, vamos arrumá-la separando a derivada do resto da equação.
Onde corresponde ao volume da esfera, e corresponde à área superficial. Assim, a razão será:
Assim:
Separando a temperatura do tempo, teremos:
Integrando dos dois lados:
Passo 3
O lado direito pode ser integrado usando o método da substituição, onde:
Logo:
Agora é só arrumar a bagunça:
Passo 4
Qual a temperatura do estado estacionário?
A temperatura do estado estacionário é dada para . Assim:
Passo 5
Determine a quantidade de calor trocada com o meio após atingir o estado estacionário.
A quantidade de calor trocada com o meio é dada por:
Substituindo a expressão que encontramos na letra :
Onde .
Ou seja, no estado estacionário, a quantidade de calor trocada com o meio será igual à quantidade de calor gerada pelo rejeito radioativo.
Resposta
Exercício Resolvido #9
Questão 4, PUCRIO, P1-2003
Uma esfera de aço , , de de diâmetro está inicialmente a temperatura uniforme igual a . A esfera é subitamente colocada num ambiente mantido a .
Faça um balanço de calor na esfera e obtenha a equação de conservação de energia, justificando as suas hipóteses. Calcule o tempo requerido para a esfera atingir , considerando que o coeficiente convectivo de troca de calor vale .
Passo 1
A equação de calor para uma superfície esférica é dada por:
Vamos utilizar as seguintes hipóteses:
- Transferência de calor somente na direção radial;
- Transferência de calor sem geração terma ;
- Propriedades térmicas constantes.
Aplicando essas simplificações, teremos:
Passo 2
Para determinar como a temperatura varia com o tempo, vamos calcular o número de Biot pra saber se vamos usar o método dos parâmetros concentrados, ou o método dos efeitos espaciais.
O número de Biot é dado por:
Opa! Como , podemos usar o método dos parâmetros concentrados.
Passo 3
Pelo método dos parâmetros concentrados, teremos o seguinte:
Onde . Assim:
Substituindo os valores:
Resposta
Exercício Resolvido #10
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
O coeficiente de transferência de calor para o ar escoando sobre uma esfera deve ser determinado pela observação do comportamento dinâmico da temperatura de uma esfera, que é fabricada em cobre puro.
A esfera, que possui de diâmetro, encontra-se a antes de ser inserida em uma corrente de ar que tem a temperatura de . Um termopar sobre a superfície externa da esfera indica após da inserção da esfera na corrente de ar.
Admita que a esfera se comporta como um objeto espacialmente isotérmico e calcule o coeficiente de transferência de calor.
Dados: , ,
Passo 1
Como temos a temperatura da esfera variando no tempo, temos um problema de condução transiente, mas não podemos calcular o Biot já que a questão não dá o coeficiente convectivo , pelo contrário, o objetivo aqui é encontrá-lo. Então como saber se podemos usar o Método dos Parâmetros Concentrados?
Não precisa se desesperar! O enunciado deu pra gente uma informação importantíssima: podemos admitir que a esfera tem comportamento espacialmente isotérmico, ou seja, a temperatura vai ser sempre uniforme na esfera inteira.
Isso é o mesmo que falar que a condução de calor da esfera é infinita, que é justamente a aproximação que a gente quer conferir se é válida quando calculamos o Biot, sendo assim, tá tudo certo, podemos usar o Método dos Parâmetros Concentrados!
Passo 2
Vamos partir então da equação do método:
Agora é só reorganizar a equação pra isolar o coeficiente convectivo h:
Passo 3
Pronto! Agora vamos substituir todos os dados que temos:
Resposta
Exercício Resolvido #11
Questão 4, UFRJ, P1-2007.1
Considere um paralelepípedo de cobre (, e ) com lados , inicialmente na temperatura uniforme de .
Este bloco de cobre é imerso em um fluido a . O coeficiente de transferência de calor entre o bloco e o fluido é de . Calcule:
Tempo necessário para que o ponto central do bloco seja resfriado até .
Taxa inicial de variação de temperatura .
Passo 1
Tempo necessário para que o ponto central do bloco seja resfriado até .
Antes de qualquer coisa, precisamos calcular o número de Biot pra decidir qual o método mais adequado pra resolver o problema.
Nesse caso, calcular o comprimento característico da seguinte forma:
Dessa forma:
Como o número de Biot é menor que 0,1, podemos usar o método dos parâmetros concentrados.
Passo 2
De acordo com o método dos parâmetros concentrados, o tempo necessário para que o bloco resfrie até será dado por:
Onde . Assim, substituindo os valores:
Passo 3
Taxa inicial de variação de temperatura .
A temperatura varia com o tempo de acordo com a expressão abaixo:
Derivando a expressão acima em relação ao tempo:
Como queremos a taxa inicial de variação de temperatura, . Assim:
Substituindo os valores:
Resposta