Teoria
Fala aí, nós somos o Responde Aí, a solução que você precisava para ter perídos tranquilos na sua faculdade. A nossa missão hoje é fazer você sair daqui sabendo o que precisa sobre empuxo parar arrasar na prova!
De forma bem geral, o empuxo é uma força que atua sobre objetos que estão parcialmente ou completamente imersos em fluidos, como a água por exemplo.
Você já se perguntou porque um navio gigantesco não afunda?

Sim, o empuxo está envolvido nesse mistério hahaha. O navio é um objeto que está imerso parcialmente na água, que é um fluido, e a água exercerá sobre o navio uma força, o empuxo. Se o empuxo for maior que o peso do navio, então o navio não afunda. O navio é todo projetado já pensando nisso, irado, não?
Definição e Fórmula do empuxo
Por definição, o empuxo é a força que o fluido exerce sobre um corpo mergulhado nele.
Imagina que temos um caixote mergulhado na água, assim:
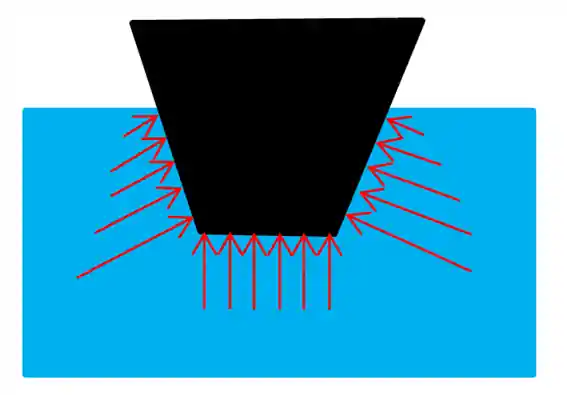
A setas vermelhas mostram as forças que a água faz em cada ponto do caixote. Se somarmos essa força obteremos uma força resultante que aponta de baixo para cima e essa força é o empuxo.
O empuxo é calculo da seguinte maneira:
Onde:
é a densidade do fluido, normalmente expressa em ; é o volume da parte do objeto que está submersa no fluido, expresso em ; é a aceleração da gravidade, que vale , e; é o empuxo, em
É importante ficar muito atento a um detalhe:

A fórmula não é complicada, mas tem que prestar atenção que a densidade que entra na fórmula é a densidade do fluido e o volume é o volume do objeto que está submerso.
Como saber se um objeto afunda ou não afunda?
Quando um corpo está imerso em um fluido as forças atuantes nele serão o peso do objeto e o Empuxo. A força resultante sobre o corpo será a soma dessas duas forças:
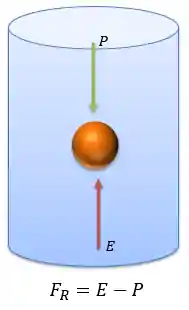
Temos três casos possíveis:
- Peso maior que empuxo
objeto afunda; - Peso igual ao empuxo
obejto fica parado em equilíbrio; - Peso menor que empuxo
objeto flutua
Exemplo
Topa fazer um exemplo aqui comigo rapidinho para fixar o conteúdo? Bora lá então
Uma esfera de raio
RESOLUÇÃO:
Vamos aplicar a fórmula do empuxo, mas para isso precisamos organizar os dados que vamos precisar.
Como a esfera está completamente imersa na água:
Como o raio é igual a
A densidade que usamos na fórmula é a do fluido, então usaremos:
E por último, precisamos da gravidade:
Vamos aplicar a fórmula então:
Prontinho!