5 - Um dormitório em uma grande universidade, construído há 50 anos, tem as paredes externas construídas com um forro, que tem e espessura . Para reduzir a perda térmica no inverno, a universidade decidiu encapsular todo o dormitório através da aplicação de uma camada de de isolante extrudado com na superfície externa do forro. O isolante extrudado é, por sua vez, coberto com vidro arquitetônico, com. Determine o fluxo térmico através das paredes original e remodelada, quando as temperaturas do ar interno e externo são e , respectivamente. Os coeficientes de transferência de calor interno e externo são e , respectivamente.
Passo 1
O desenho que demonstra a distribuição térmica e o circuito térmico equivalente para uma parede composta em série, é mostrado abaixo.

Passo 2
Agora vamos calcular o fluxo de calor através das paredes adaptadas usando a equação mostrada abaixo.
Aqui, a condutividade térmica do revestimento é , a condutividade térmica do isolamento estendido é , o vidro arquitetônico da condutividade térmica é , a espessura do revestimento é , a espessura do isolamento extrudado é , a espessura do vidro arquitetônico é , o coeficiente de transferência de calor convectivo interior é , o coeficiente de transferência de calor convectivo externo é e as temperaturas interna e externa são e .
Substituindo pelos valores fornecidos, temos:
Portanto, o fluxo de calor que flui através das paredes adaptadas é .
Passo 3
Agora vamos desenhar a distribuição térmica e o circuito térmico equivalente para uma parede plana, como mostrado abaixo.
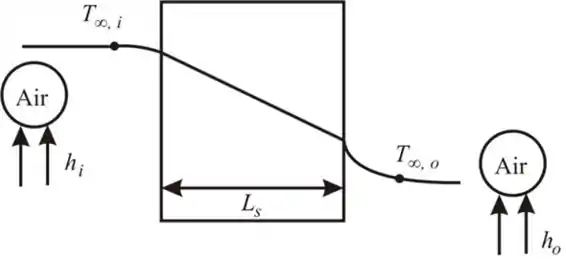
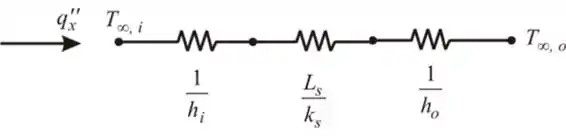
Passo 4
Podemos calcular o fluxo de calor através da parede original usando a equação mostrada abaixo.
Substituindo pelos valores conhecidos, temos:
Portanto, o fluxo de calor flui através da parede original é .
Resposta
O fluxo de calor que flui através das paredes adaptadas é .
O fluxo de calor flui através da parede original é