4 - O vidro traseiro de um automóvel é desembaçado pela fixação de um aquecedor em película, fino e transparente, sobre a sua superfície interna. Aquecendo eletricamente este elemento, um fluxo térmico uniforme pode ser estabelecido na superfície interna.

(a) Para um vidro com de espessura, determine a potência elétrica, por unidade de área do vidro, necessária para manter uma temperatura na superfície interna de , quando a temperatura do ar no interior do carro e o coeficiente convectivo são e , enquanto a temperatura e o coeficiente convectivo no ar exterior (ambiente) são e .

(b) Na prática, e variam de acordo com as condições climáticas e com a velocidade do carro. Para valores de , determine e represente graficamente a potência elétrica necessária como uma , de para . Com base em seus resultados, o que você pode concluir a respeito da necessidade de operação do aquecedor a baixos valores de ? Como essa conclusão é afetada pelo valor de ? Se , em que é a velocidade do veículo e é um expoente positivo, como a velocidade do veículo afeta a necessidade de operação do aquecedor?

Aplique o balanço de energia na superfície interna da janela da seguinte maneira:

Aqui,  é a quantidade de fluxo de calor da temperatura do ar interior para a temperatura da superfície interna,  é a temperatura da superfície interna,  é a temperatura do ar ambiente,  é a espessura da janela de vidro,  é a condutividade térmica do vidro e  é o coeficiente de convecção do ar ambiente.

Obtenha a condutividade térmica do vidro na tabela A.3, “Propriedades termofísicas de materiais comuns” no livro a temperatura de .

Determine o fluxo de calor por convecção na superfície interna da janela da seguinte maneira:

Aqui  é a temperatura do ar interior e  é o coeficiente de transferência de calor interior do ar.

Substituindo pelos valores fornecidos, temos:

Encontre o fluxo de calor uniforme por meio da equação .

Portanto, a energia elétrica necessária é .

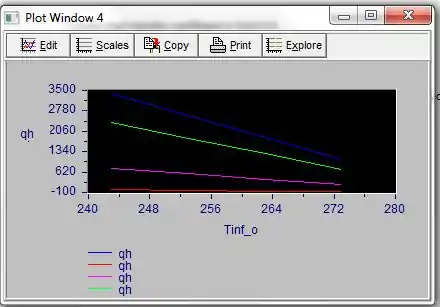
O gráfico foi plotado entre a potência do aquecedor e a temperatura ambiente da seguinte maneira:

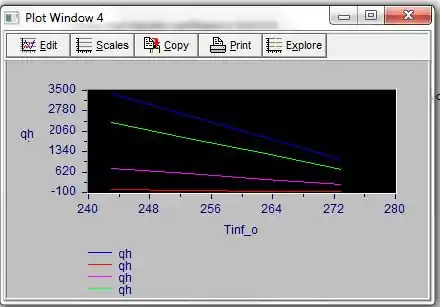
A linha de cor vermelha indica variação do fluxo de calor quando .

A linha Pink Color indica variação do fluxo de calor quando 

A linha de cor verde indica variação do fluxo de calor quando 

A linha de cor azul indica variação do fluxo de calor quando 

No gráfico, observe que 

O aquecedor não é necessário.

Se o coeficiente de transferência de calor for proporcional à velocidade da potência do expoente . , o requisito de energia térmica aumenta porque, quando a velocidade do veículo aumenta, a transferência de calor por convecção também aumenta.