Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 86
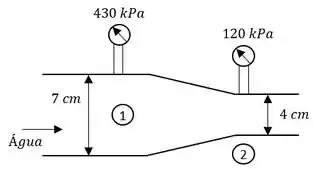
A água escoa através de um medidor Venturi cujo diâmetro é de 7 cm na parte da entrada e de 4 cm na garganta. A pressão é medida como 430 kPa na entrada e 120 kPa na garganta. Desprezando os efeitos do atrito, determine a vazão da água.
Passo 1
Oi pessoal, tudo bem?
Bem, assumimos inicialmente que:
1. O fluxo através do Venturi é constante, incompressível e não rotacional com atrito desprezível (de modo que a equação de Bernoulli é aplicável).
2. O fluxo é horizontal, de modo que a elevação ao longo da linha central é constante.
3. A pressão é uniforme em uma determinada seção transversal do medidor de Venturi (ou os efeitos de elevação na medição de pressão são desprezíveis).
E devemos lembrar que:
Passo 2
Pronto, agora vamos analisar o problema, ok?
Assim, tomamos o ponto 1 na seção de fluxo principal e o ponto 2 na garganta ao longo da linha central do medidor de Venturi (observar na figura). Observando que , a aplicação da equação de Bernoulli entre os pontos 1 e 2 fornece:
O fluxo é assumido como incompressível e, portanto, a densidade é constante. Então a relação de conservação de massa para esse dispositivo de fluxo constante de fluxo único pode ser expresso como:
Assim, podemos dizer que:
Passo 3
Podemos, portanto, substituir os valores das velocidades da equação 1, assim:
Reorganizando os termos deixando a vazão em evidência, temos:
A vazão para o caso em questão pode ser determinada substituindo os valores fornecidos nessa relação por:
Resposta
Portanto: