Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 27

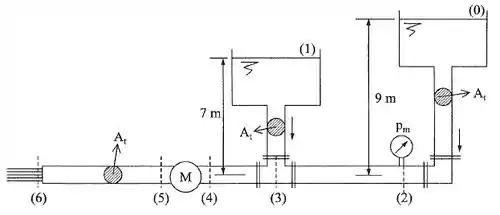
Sabendo que a vazão proporcionada pelo tanque inferior da instalação é igual a 15 L/s e que a potência dissipada por atritos em toda a instalação é 1 kW, determinar o tipo da máquina e sua potência. Dados: γ = 10 4   N / m 3 ; H p 0,2 = 4,8   m ; A t = 100   c m 2 ; p m = 40   k P a ; η m = 80 % .

Passo 1

Vamos começar o exercício aplicando o equilíbrio de cargas entre os pontos 0 e 2:

H 0 = H 2 + H p 0,2

Abrindo a expressão, temos:

α 0 v 0 2 2 g + p 0 γ + z 0 = α 2 v 2 2 2 g + p 2 γ + z 2 + H p 0,2

Agora vamos isolar v 2 e substituir os valores conhecidos:

α 2 v 2 2 2 g = α 0 v 0 2 2 g + p 0 γ + z 0 - p 2 γ + z 2 + H p 0,2

v 2 2 = 2 g α 2 α 0 v 0 2 2 g + p 0 γ + z 0 - p 2 γ + z 2 + H p 0,2

v 2 2 = 2 ( 10 ) 1 α 0 0 2 ( 10 ) + 0 10 4 + 0 - 40.10 3 10 4 - 9 + 4,8 → v 2 = 2   m / s

Passo 2

Agora vamos encontrar a vazão no ponto 0 e no ponto 6, começando pelo ponto 0, temos:

Q 0 = v 2 A t = 2 100.10 - 4 → Q 0 = 0,02   m 3 / s

E, pelo desenho, sabemos que a vazão total no ponto 6 será a soma das vazões no ponto 0 e no ponto 1, então, temos:

Q 6 = Q 0 + Q 1 = 0,02 + 15.10 - 3 → Q 6 = 0,035   m 3 / s

Agora, tendo a vazão no ponto 6, podemos encontrar a velocidade nesse ponto:

Q 6 = v 6 A t → v 6 = Q 6 A t = 0,035 100.10 - 4 → v 6 = 3,5   m / s

E, com a velocidade no ponto 6, podemos usar a equação da carga cinética para encontrar a carga nesse ponto (já que nesse ponto só temos componente cinética):

H 6 = α 6 v 6 2 2 g = 1 3,5 2 2 10 → H 6 = 0,612   m

Passo 3

Agora, vamos usar o princípio da conservação da energia para o sistema, dessa forma, temos:

γ Q 0 H 0 + γ Q 1 H 1 + N = γ Q 6 H 6 + N d i s s i p a d o

Substituindo os valores conhecidos na equação, temos:

10 4 0,02 9 + 10 4 0,015 7 + N = 10 4 0,035 0,612 + 1.10 3 → N = - 1635,8   W

Como a potência cedida ao fluido é negativa, ou seja, na verdade o fluido cede potência à máquina, temos então uma turbina, e sua potência real será:

N T = η m N = 0,8 1635,8 → N T = 1308,6   W

Resposta

N T = 1308,6   W   ( t u r b i n a )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar escoa isotermicamente por um tubo longo, horizontal, de diâmetro constante. Numa seção em que a pressão é de 1MPa (abs), a velocidade é 25 m/s. Por causa do atrito no escoamento, a pressão numa seç
Uma turbina a vapor consome 4500 kg/h de vapor e recebe dele 736 kW. As velocidades de entrada e saída do vapor são, respectivamente, 60 m/s e 275 m/s, e as entalpias, 2760 kJ/kg e 2090 kJ/kg. Calcula
A figura mostra uma máquina hidráulica por onde escoa água, isotermicamente. Desprezando as diferenças de cotas, determinar o tipo de máquina e o seu rendimento. Dados: A 1 = 0,5m 2 ; A 2 = 0,2m 2 ; A
No convergente da figura escoa ar considerado gás perfeito. Sendo A 1 = 0,1m 2 ; A 2 = 0,05m 2 ; p 1 = 0,2M P aa b s ; p 2 = 0,1M P aa b seρ 1 = 1k g / m 3 , determinar o calor trocado entre (1) e (2)
No sistema da figura, a bomba deve fornecer 10 L/s ao reservatório superior e a turbina deve ter uma potência no eixo de 3 kW com um rendimento de 80%. Qual é a carga manométrica da bomba e a da turbi