Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 16
16. Condução de calor unidimensional, em regime estacionário, ocorre em uma barra de condutividade térmica constante k e área da seção transversal variando conforme a relação Ax(x) = Aoeax, na qual Ao e a são constantes. A superfície lateral da barra encontra-se isolada termicamente.
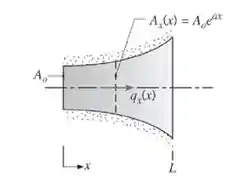
(a) Escreva uma expressão para a taxa de condução de calor, qx(x). Use essa expressão para determinar a distribuição de temperaturas T(x) e esboce,qualitativamente, a distribuição para T(0) > T(L).
(b) Agora considere condições nas quais há geração de energia térmica no interior da barra a uma taxa volumétrica de = exp(−ax), na qual o é uma constante. Obtenha uma expressão para qx(x), quando a face esquerda da barra (x = 0) se encontra isolada termicamente.
Passo 1
Desenvolva a expressão para taxa de transferência de calor por condução a partir da equação do balanço energético:
Fazendo algumas substituições na equação acima chegamos em:
Passo 2
Letra (a)
Considere o caso em que não há geração de calor na haste, temos da equação (1):
Assim, a expressão para a temperatura na barra é
O gráfico que mostra a variação de temperatura com a posição é o seguinte:
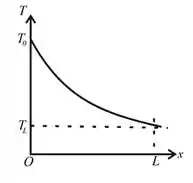
Passo 3
Letra (b)
Considere o caso em que há geração de calor na haste e modifique a equação (1):
Assim, a expressão para a taxa de transferência de calor na haste é