Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 68
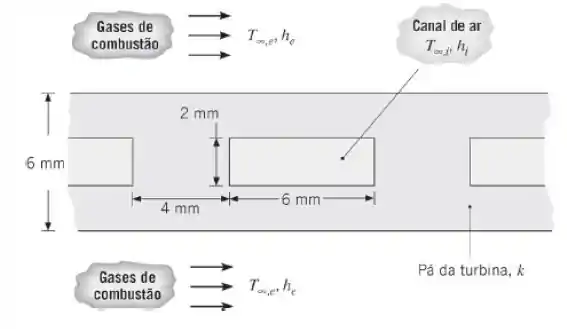
Seja o sistema para resfriamento de turbina a gás mostrado no Exemplo 4.3. No Problema 3.23 são descritas vantagens associadas à aplicação de um revestimento de barreira térmica (RBT) sobre a superfície exterior da pá da turbina. Se um revestimento de zircônia com 0,5 mm de espessura for aplicado sobre a superfície externa da pá resfriada com ar, determine o campo de temperaturas na pá para as condições operacionais do Exemplo 4.3.
Passo 1
Boom galerinha, vamos começar?
Vamos começar desenhando o que está acontecendo neste problema, no desenho do Exemplo 4.3 que nós vimos acima:
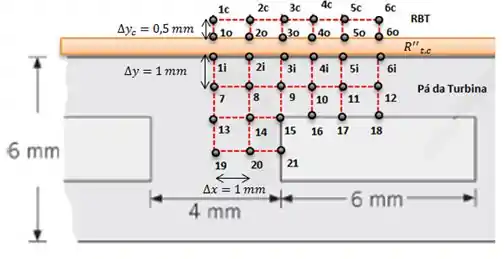
Nós precisamos das temperaturas, então vamos começar com os nós c, ok?
Nestes casos nós temos uma expressão do tipo:
Sabendo que:
Substituindo:
Para 1c:
Para 2c:
Para 3c:
Para 4c:
Para 5c:
Para 6c:
Agora nós precisamos das temperaturas nos nós o, ok?
Nestes casos nós temos uma expressão do tipo:
Substituindo:
Para 1o:
Para 2o:
Para 3o:
Para 4o:
Para 5o:
Para 6o:
Passo 2
Agora nós precisamos das temperaturas nos nós I, ok?
Nestes casos nós temos uma expressão do tipo:
Sabendo que:
Substituindo:
Para 1i:
Para 2i:
Para 3i:
Para 4i:
Para 5i:
Para 6o:
Os demais pontos nós podemos usar as equações dadas no Exemplo 4.3. Para os pontos internos:
Para o Ponto 15, um vértice interno:
Colocando nossos valores nos termos:
Então:
Para o Ponto 16 e 17, na superfície plana com convecção:
Para o Ponto 18 e 21:
Quando resolvemos as equações simultâneas:
E o que seria de nós sem softwares?!
Nem seeei !!
E ficamos por aqui galerinhaa !!