Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 83

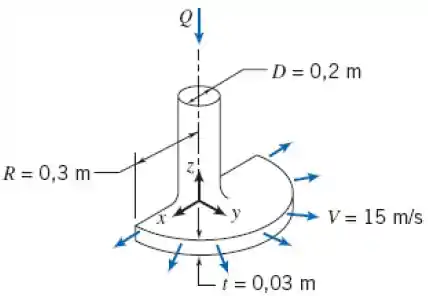
4.83 O bocal mostrado descarrega uma cortina de água por meio de um arco de 180°. A uma distância radia de 0,3 m a partir da linha de centro do tubo de suprimento, a velocidade da água é 15 m/s e a espessura do jato é 30 mm. Determine (a) a vazão volumétrica da cortina de água e (b) a componente y da força necessária para manter o bocal no lugar.

Passo 1

(a) Como a velocidade de saída é 15 m/s e também sabemes a área pela qual a água sai, então:

Q = v 2 A 2

Sendo:

A 2 = π R t

Então:

Q = V 2 π R   t

Q = 15 π 0,3 0,03

Q = 0,424   m 3 / s

Passo 2

(b) Aqui vamos usar somente a componente y da equação de momento:

F R y + F B y = ∂ ∂ t ∫ V C v ρ   d V + ∫ C V v ρ V → d A →                          

Como é regime permantente, então:

∂ ∂ t ∫ V C v ρ   d V = 0                  

PRESTANDO ATENÇÃO para não cair na pegadinha dos eixo, pois y é a componente horizontal...

Então vamos ver algo que descreva a velocidade em y.

É razoavel pensar em:

V y = V cos ⁡ θ

Onde θ varia de - π 2 , + π 2 .

Desprezando as forças de campo,

F B y = 0

Considerando que somente tem a pressão atmosférica (p=0),

R y = ∫ - π 2 π 2 V cos ⁡ θ V ρ R t d θ

R y = 2 ρ V 2 R t

R y = 4050   N

Resposta

(a) Q = 0,424   m 3 / s

(b)

R y = 4050   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma turbina de ação do tipo Pelton, tem-se os seguintes dados: raio da turbina: R = 1,5 m; rotação: 450 rpm; ângulo de saída das pás: 170°; velocidae do jato: 100 m/s; área da seção do jato: 0,1
A água que sai de um reservatório de grandes dimensões penetra num conduto de 15 cm de diâmetro e incide sobre uma pá defletora fixa que desvia o jato de 90°, conforme a figura. Sabendo que o empuxo h
O jato de água ( ρ = 1000k g / m 3 ) de área A j = 10 - 4m 2 incie com velocidade v j na pá solidária ao carro, que se move sem atrito num plano horizontal. O carro, ao se mover, por ação do jato, reb
O bocal da esquerda tem uma área de 30 cm² e lança um jato com velocidade de 10 m/s contra a pá. O sistema está em equilíbrio. Qual é a vazão do segundo bocal e qual é a velocidade do jato se a área d
O desviador de jato da figura move-se sobre o plano inclinado com velocidade de 1,0 m/s. Sabendo que seu peso é 200 N, que sua base é 1,0 m² e que entre o desviador e o plano inclinado existe uma cama