Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 86

4.86 Considere o escoamento através da expansão súbita mostrada. Se o escoamento for incompressível e o atrito desprezível, mostre que o aumento de pressão, Δ p = p 2 - p 1 , é dado por Δ p 1 2 ρ V - 1 2 = 2 d D 2 1 - d D 2 . Trace o gráfico do aumento de pressão adimensional versus a razão de diâmetros para determinar o valor ótimo de d / D e o valor correspondene do aumento adimensional de pressão. Sugestão: Suponha que a pressão seja uniforme e igual a p 1 na superfície vertical da expansão.

Passo 1

Vamos tomar como volume de controle somente a parte entre 1 e 2, logo depois da expansão.

Começando pela equação de quantidade de movimento:

F → = F → R + F → B = ∂ ∂ t ∫ V C V → ρ   d V + ∫ S C V → ρ V → ⋅ d A →

Como o escoamento é em regime permanente,

∂ ∂ t ∫ V C V → ρ   d V = 0

Vamos desprezar o peso do compartimento e o peso da água dentro do compartimento, então:

F → B = 0

A componente x da equação de quantidade de movimento fica, então:

F → R x = ∫ A 1 u ρ V → ⋅ d A →

R x + p 1 A 2 - p 2 A 2 = V 1 - ρ V 1 A 1 + V 2 ρ V 2 A 2

Atenção aqui porque o volume de controle é todo com área A 2 , mas aparece A 1 porque ele é referente à vazão que sai da parte mais fina.

Como o atrito é desprezível,

R x = 0

Então, ficamos com:

p 1 A 2 - p 2 A 2 = V 1 - ρ V 1 A 1 + V 2 ρ V 2 A 2

Pela equação da continuidade podemos achar V 2 em função de V 1 :

V 1 A 1 = V 2 A 2

V 2 = V 1 A 1 A 2

Então:

p 1 A 2 - p 2 A 2 = V 1 - ρ V 1 A 1 + V 1 A 1 A 2 ρ V 1 A 1 A 2 A 2

A 2 p 2 - p 1 = - - ρ V 1 2 A 1 + ρ V 1 2 A 1 2 A 2

A 2 p 2 - p 1 = ρ V 1 2 A 1 - A 1 2 A 2

p 2 - p 1 = ρ V 1 2 A 1 A 2 - A 1 2 A 2

Como A 1 = π d 2 2 e A 2 = π D 2 2 ,

p 2 - p 1 = ρ V 1 2 π d 2 2 π D 2 2 - π d 2 2 2 π D 2 2 2

p 2 - p 1 = ρ V 1 2 d D 2 - d D 2 2

Agora vamos forçar pra achar a expressão que ele quer, ne...

Δ p = 1 2 ρ V 1 2 2 d D 2 - d D 2 2

Δ p 1 2 ρ V 1 2 = 2 d D 2 - d D 2 2

Δ p 1 2 ρ V 1 2 = 2 d D 2 1 - d D 2

Como queríamos demonstrar.

Passo 2

Plotando:

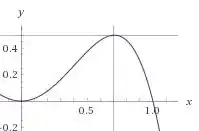
Podemos dizer que d D m á x = 0,7   e seu valor correspondente para o aumento de pressão adimensional é 0,5.

Resposta

d D m á x = 0,7   e seu valor correspondente para o aumento de pressão adimensional é 0,5.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fabricante de brinquedos constrói um carrinho impulsionado pelo ar de uma bexiga. No instante inicial em que é liberado o ar, determinar:a) a força de propulsão;b) a pressão do ar da bexiga, despre
Sabendo que o sistema da figura encontra-se em equilíbrio, desprezando as perdas, determinar a altura h 0 . ( γ H 2 O = 10 4N / m 3 ; γ = 2.10 4N / m 3 ; A p = 8.10 - 3m 2 ; h 1 = 78,5c m ; Q = 15,7L
No tanque da figura, determinar a força F s x que deve ser aplicada para que ele permaneça parado. Qual é o diâmetro do bocal que deverá ser instalado na parede oposta ao bocal mostrado na figura, par
Considerando que na região de escoamento completamente desenvolvido de um tubo, a integral da quantidade de movimento axial é a mesma em todas as seções transversais, explique a razão para a queda de
Para as condições do Problema 4.34, avalie a razão entre o fluxo de quantidade de movimento na direção x na saída do canal e aquele na entrada.