Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 87
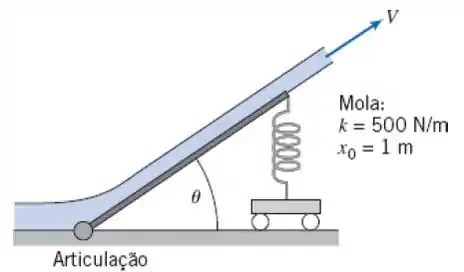
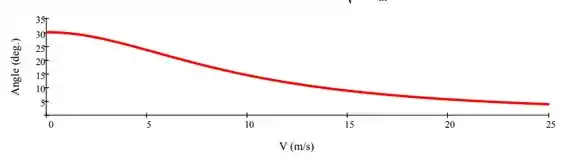
4.87 Um jato livre de água, com área de seção transversal constante e igual a 0,01 m², é defletido por uma placa suspensa de 2 m de comprimento, suportada por uma mola com constante e o comprimento normal . Determine e trace um gráfico do ângulo de deflexão como uma função da velocidade do jato . Qual velocidade do jato tem ângulo de deflexão ?
Passo 1
Sabendo que a força da mola é
Onde .
Aplicando, então, a equação da quantidade de movimento na vertical:
Passo 2
Para o ângulo de 5° ():
Resposta
Exercícios de Livros Relacionados
O tubo (2)-(3) da figura está ligado ao tanque por meio de uma junta elástica de borracha que impede a transferência de esforços entre o tanque e o tubo. Calcular a altura h do nível de água do tanque
Calcular o esforço horizontal sobre a estrutura do ventilador da figura e a potência transmitida ao fluido pelo ventilador. Desprezar a perda de carga entre as seções (1) e (2). Dados: D 2 = 0,38m ; v
Calcular a força horizontal aplicada sobre o suporte do bocal da figura. Sabendo que a água incide na placa, plana e vertical, e se distribui igualmente em todas as direções, calcular a força que deve
No trecho (1)-(2) da tubulação, que está num plano horizontal, escoa água em regime permanente. A perda de carga de (1) a (2) é 10 m e a vazão, 10 L/s. Qual é a força resultante aplicada pelo fluido n
Na instalação esquematizada na figura, (T) é uma turbina e o fluido que escoa é água de massa específica ρ = 1000k g / m 3 . A vazão que escoa é 314 L/s e as pressões em (1) e (2) são, respectivamente