4.89 A figura mostra um redutor em uma tubulação. O volume interno do redutor é 0,2 m³ e a sua massa é 25 kg. Avalie a força total de reação que deve ser feita pelos tubos adjacentes para suportar o redutor. O fluido é a gasolina.
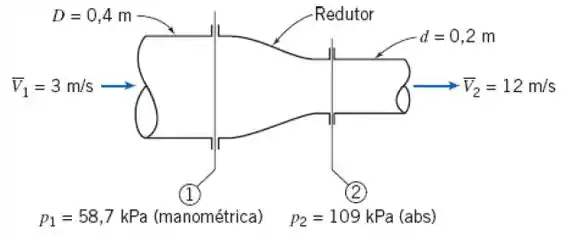
Passo 1
Vamos começar pela equação de quantidade de movimento:
Como o escoamento é em regime permanente,
Vamos primeiro calcular a componente x (, pois não tem força de campo em x):
Sendo, e ,
Na tabela A.2 do do Apêndice A temos a densidade relativa da gasolina igual a 0,72, então, como a densidade da água é 999 kg/m³,
Substituindo:
Ps: Como a pressão 2 é absoluta temos que tirar 101000 Pa da pressão atmosférica.
Tem o sinal negativo, pois admitimos tudo para direita, mas, na verdade é pra esquerda.
Passo 2
Agora vamos calcular a componente y (já em y só tem ):