Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 4

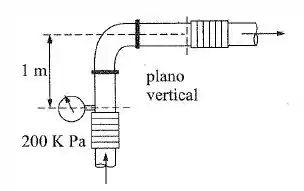
O cotovelo da figura está preso por duas luvas elásticas para que não seja influenciado pelo resto da instalação. Sendo a área de sua seção 20 cm² e a vazão 20 L/s, qual será a força causada pelo escoamento do fluido se a perda de carga é 1,0 m ( ρ = 1000   k g / m ^ 3 ) ?

Passo 1

Vamos começar o exercício calculando a velocidade nos pontos 1 e 2, como a vazão é constante e área da seção também, as velocidades serão iguais nesses pontos, então:

v 1 = v 2 = Q A = 20.10 - 3 20.10 - 4 → v = 10   m / s

Agora podemos calcular a vazão mássica que passa pelo cotovelo:

Q m = ρ Q = 1000 20.10 - 3 → Q m = 20   k g / s

Agora vamos aplicar a equação para o equilíbrio de cargas entre os pontos 1 e 2:

H 1 = H 2 + H p 1,2

v 1 2 2 g + p 1 γ + z 1 = v 2 2 2 g + p 2 γ + z 2 + H p 1,2

Substituindo os valores conhecidos, temos:

10 2 2 10 + 200.10 3 10 4 + 0 = 10 2 2 10 + p 2 10 4 + 1 + 1 → p 2 = 10 4 20 - 2 → p 2 = 180   k P a

Passo 2

Agora vamos analisar a força aplicada ao cotovelo. A equação que representa a força que o fluido exerce é dada por:

F → s = - p 1 A 1 n → 1 + p 2 A 2 n → 2 + Q m v → 2 - v → 1

Agora vamos calcular a componente em x ( → ) :

F s x = - p 1 A 1 0 + p 2 A 2 1 + Q m v 2 - 0

Substituindo os valores conhecidos:

F s x = - 0 + 180.10 3 20.10 - 4 1 + 20 10 → F s x = - 560   N

Agora vamos calcular a componente em z ( ↑ ) :

F s z = - p 1 A 1 - 1 + p 2 A 2 0 + Q m 0 - v 1

Substituindo os valores conhecidos:

F s z = - 200.10 3 20.10 - 4 - 1 + 0 + 20 - 10 → F s z = 600   N

Passo 3

Agora, só precisamos encontrar o módulo da força, que é dado por:

F s 2 = F s x 2 + F s z 2 → F s = F s x 2 + F s z 2

Substituindo os valores encontrados no passo 2:

F s = - 560 2 + 600 2 → F s = 820,7   N

Resposta

F s = 820,7   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Jatos de água estão sendo usados cada vez com maior frequência para operações de cortes de metais. Se uma bomba gera uma vazão de 63 x 10 - 6m 3 / s através de um orifício de diâmetro 0,254m m , qual
Avalie a taxa líquida de fluxo de quantidade de movimento para fora da superfície de controle do Problema 4.24.
Um fazendeiro compra 675k g de grãos, a granel, da cooperativa local. Os grãos são despejados na sua caminhonete através de um alimentador afunilado com um diâmetro de saída de 0,3m . O operador do al
Água escoa em regime permanente pelo bocal de uma mangueira de incêndio. A mangueira tem diâmetro interno de 75m m e a ponta do bocal de 25m m ; a pressão manométrica na mangueira é 510k P a e a corre
Um tipo de prato, raso e circular, tem um orifício de bordas vivas no centro. Um jato de água, de velocidade V , atinge o prato concentricamente. Obtenha uma expressão para a força externa necessária