Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 7
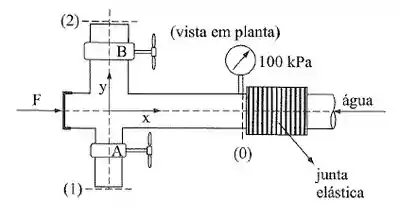
No esquema que segue, podem ocorrer duas situações:
1) o registro (B) fechado e o registro (A) aberto, a água é despejada por (1);
2) o registro (A) fechado e o registro (B) aberto, a água é despejada por (2).
Em ambos os casos, a pressão indicada na figura é a mesma, bem como se tem a mesma força , necessária para o equilíbrio segundo a direção x. Determinar, para cada uma das situações citadas, qual deve ser a força para o equilíbrio, segundo a direção y.
Dados: ; .
Passo 1
Pelo desenho, sabemos que toda a água que entra por 0, sai por 1 ou 2, então, como a vazão é a mesma, temos:
Agora podemos escrever a vazão mássica do sistema:
Aplicando a equação para a força exercida pelo fluido, dada por:
Vamos aplicar a equação na direção :
Substituindo os valores conhecidos, temos:
Assim, a vazão mássica é dada por:
E a vazão volumétrica é:
Passo 2
Agora vamos encontrar o valor das velocidades em 1 e 2 através da vazão (que será a mesma para ambos os casos):
Passo 3
Agora iremos aplicar novamente a equação da força, só que agora analisando para o caso 1, entre os pontos 0 e 1, a equação se torna:
Agora vamos calcular a componente em :
Substituindo os valores conhecidos:
Agora, da mesma forma, só que para o caso 2, entre os pontos 0 e 2, a equação se torna:
Agora vamos calcular a componente em :
Substituindo os valores conhecidos: