Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 54
54. Para melhorar a dissipação térmica em um chip de silício, quadrado com W = 4 mm, um pino de cobre é fundido à superfície do chip. O comprimento e o diâmetro do pino são L = 12 mm e D = 2 mm, respectivamente, e ar atmosférico a V = 10 m/s e T∞ = 300 K está em escoamento cruzado em relação ao pino. A superfície do chip e, portanto, a base do pino, é mantida a uma temperatura de Tb = 350 K.
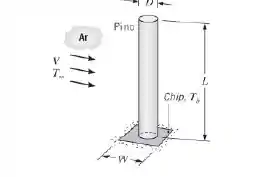
(a) Supondo que o chip cause um efeito desprezível sobre o escoamento ao redor do pino, qual é o coeficiente convectivo médio na superfície do pino?
(b) Desprezando a radiação e supondo que o coeficiente convectivo na extremidade do pino seja igual ao calculado na parte (a), determine a taxa de transferência de calor no pino.
(c) Desprezando a radiação e supondo que o coeficiente de transferência de calor na superfície exposta do chip seja igual ao calculado na parte (a), determine a taxa total de transferência de calor saindo do chip.
(d) Independentemente, determine e represente graficamente o efeito de aumentos na velocidade (10 ≤ V ≤ 40 m/s) e no diâmetro do pino (2 ≤D ≤ 4 mm) na taxa total de transferência de calor saindo do chip. Qual é a taxa de transferência de calor para V = 40 m/s e D = 4 mm?
Passo 1
Primeiro devemos Calcular a temperatura média do filme.
Obtenha as propriedades do ar na tabela A.4, “Propriedades termo-físicas dos gases à pressão atmosférica”, à temperatura .
A viscosidade cinemática é,
O coeficiente de condutividade térmica é,
O número Prandtl é,
Obtenha a condutividade térmica ( k ) para aço inoxidável
Calcule o número de Reynolds.
Como o número de Reynolds é , o fluxo é laminar.
Considere a seguinte relação:
Aqui, a equação de Churchill e Bernstein é válida.
Considere a seguinte expressão para o número de Nusselt pela equação "Churchill e Bernstein":
Ao substituir os valores temos que:
Passo 2
Letra (a)
Calcule o coeficiente de convecção médio para a superfície da aleta da seguinte forma:
Portanto, o coeficiente de convecção médio é .
Passo 3
Letra (b)
Calcule o valor do seguinte:
Calcule o valor do seguinte:
Calcule a taxa de transferência de calor dos pinos usando a seguinte relação:
Portanto, a taxa de transferência de calor é .
Passo 4
Letra (c)
Calcule a transferência de calor da base da seguinte maneira:
Aqui está a largura da placa de base.
Calcule a taxa total da transferência de calor usando a seguinte relação:
Portanto, a transferência de calor será .