Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 46

Considere os fluidos a seguir, cada um com uma velocidade de V = 5 m/s e uma temperatura de T ∞ = 20 °C, em escoamento cruzado sobre um cilindro com 10 mm de diâmetro, mantido a 50 °C: ar atmosférico, água saturada e óleo de motor.

(a) Calcule a taxa de transferência de calor por unidade de comprimento do cilindro, q′, usando a correlação de Churchill–Bernstein.

(b) Gere um gráfico de q′ como uma função da velocidade do fluido para 0,5 ≤ V ≤ 10 m/s.

Passo 1

Tá legal, vamos começar a letra (a) calculando o valor da temperatura de filme T f que será:

T f = 20 + 50 2 → T f = 35   ° C = 308   K

Agora nós vamos para o apêndice A pegar as informações de cada um dos fluidos, na temperatura de filme, que vamos utilizar. Começando com o ar, da tabela A.4, temos:

k = 0,0269   W / m . K

ν = 16,69 . 10 - 6   m 2 / s

P r = 0,706

Agora, da tabela A.6 conseguimos as informações da água saturada, onde teremos:

k = 0,625   W / m . K

ρ = 994   k g / m 3

μ = 725.10 - 6   N . s / m 2

P r = 4,85

E, por fim, da tabela A.5 temos as informações do óleo de motor, que serão:

k = 0,145   W / m . K

ν = 340 . 10 - 6   m 2 / s

P r = 4000

Passo 2

Agora, com todas as propriedades determinadas, nós temos que encontrar a taxa de transferência de calor por unidade de comprimento do cilindro. Para isso, temos que utilizar a relação para o número de Nusselt pedida no enunciado, que é dada por:

N u - D = 0,3 + 0,62 R e D 1 2 P r 1 3 1 + 0,4 P r 2 3 1 4 1 + R e D 282000 5 8 4 5

Para calcular esse número de Nusselt, vamos precisar do número de Reynolds, que é dado por:

R e D = V D ν = ρ V D μ

Depois de calculado o número de Nusselt, vamos utilizar a relação entre ele e o coeficiente convectivo, que é dada por:

h - = k N u - D D

Para encontrar o coeficiente convectivo, feito isso podemos calcular a taxa de transferência de calor por unidade de comprimento, dada pela equação:

q ' = h π D T s - T ∞

Passo 3

Com o passo a passo descrito no passo 2, vamos começar com o ar atmosférico, então, seu número de Reynolds será:

R e D = V D ν = 5 0,01 16,69.10 - 6 → R e D = 2995,8

Substituindo esse valor e o número de Prandtl na equação para Nusselt, temos:

N u - D = 0,3 + 0,62 2995,8 1 2 ( 0,706 ) 1 3 1 + 0,4 0,706 2 3 1 4 1 + 2995,8 282000 5 8 4 5

N u - D = 28,1

Agora, substituindo esse valor de Nusselt na equação para o coeficiente convectivo, temos:

h - = k N u - D D = 0,0269 28,1 0,01 → h - = 75,5   W / m 2 . K

E, por fim, substituindo os valores conhecidos na equação para a taxa de transferência de calor, chegamos em:

q ' = h π D T s - T ∞ = 75,5 π 0,01 50 - 20 → q a r ' = 71,1   W / m

Passo 4

Repetindo o processo para a água saturada, começando por Reynolds, temos:

R e D = ρ V D μ = 994 5 0,01 725.10 - 6 → R e D = 68551,7

Substituindo esse valor e o número de Prandtl na equação para Nusselt, temos:

N u - D = 0,3 + 0,62 68551,7 1 2 ( 4,85 ) 1 3 1 + 0,4 4,85 2 3 1 4 1 + 68551,7 282000 5 8 4 5

N u - D = 347

Agora, substituindo esse valor de Nusselt na equação para o coeficiente convectivo, temos:

h - = k N u - D D = 0,625 347 0,01 → h - = 21687,5   W / m 2 . K

E, por fim, substituindo os valores conhecidos na equação para a taxa de transferência de calor, chegamos em:

q ' = h π D T s - T ∞ = 21687,5 π 0,01 50 - 20 → q á g u a ' = 20440   W / m

Passo 5

E, por fim, o processo para o óleo, começando por Reynolds, temos:

R e D = V D ν = 5 0,01 340 . 10 - 6 → R e D = 147

Substituindo esse valor e o número de Prandtl na equação para Nusselt, temos:

N u - D = 0,3 + 0,62 147 1 2 ( 4000 ) 1 3 1 + 0,4 40000 2 3 1 4 1 + 147 282000 5 8 4 5

N u - D = 120

Agora, substituindo esse valor de Nusselt na equação para o coeficiente convectivo, temos:

h - = k N u - D D = 0,145 120 0,01 → h - = 1740   W / m 2 . K

E, por fim, substituindo os valores conhecidos na equação para a taxa de transferência de calor, chegamos em:

q ' = h π D T s - T ∞ = 1740 π 0,01 50 - 20 → q ó l e o ' = 1639,9   W / m

Passo 6

Agora, para gerar um gráfico da taxa de transferência de calor por unidade de comprimento em função da velocidade, o que precisamos fazer é realizar os mesmos cálculos feitos nos passos 3 a 5, para diferentes valores de velocidade. Fazendo isso, chegaremos no seguinte gráfico:

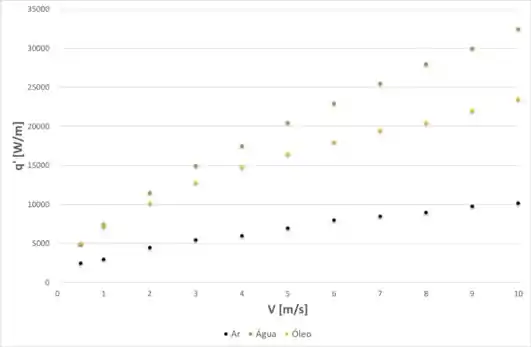
A única coisa que tivemos que fazer foi multiplicar o valor das taxas de transferência de calor do ar por 100 e do óleo por 10, para manterem os dados em uma mesma escala. Então, para obter o valor real, deve-se dividir o calor trocado através do ar por 100 e o do óleo por 10.

Resposta

q a r ' = 71,1   W / m

q á g u a ' = 20440   W / m

q ó l e o ' = 1639,9   W / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

53. Ar, a 27°C e com uma velocidade de 5 m/s, passa sobre a pequena região As (20 mm × 20 mm) de uma grande superfície, que é mantida a Ts = 127°C. Nessas condições, uma taxa de 0,5 W é removida da su
55. Seja o fio de níquel cromo (D = 1 mm, ρe = 10−6 Ω · m, k = 25 W/(m · K), ε = 0,20) usado para fabricar o aquecedor de ar do Problema 3.86, mas agora sob condições nas quais o coeficiente de transf
O objetivo de um experimento executado por estudantes é o de determinar o efeito da presença de pinos (aletas piniformes) na resistência térmica entre uma placa plana e uma corrente de ar. Uma placa q
Considere o processo de pulverização de plasma discutido nos Problemas 5.25 e 7.82. Para um diâmetro de saída do bocal de D = 10 mm e um raio do substrato de r = 25 mm, estime a taxa de transferência
Uma sonda criogênica é usada para tratar tecido cutâneo canceroso. A sonda é constituída por um único jato circular de diâmetro Dsai = 2 mm emanado de um bocal encapsulado concentricamente no interior