Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 80

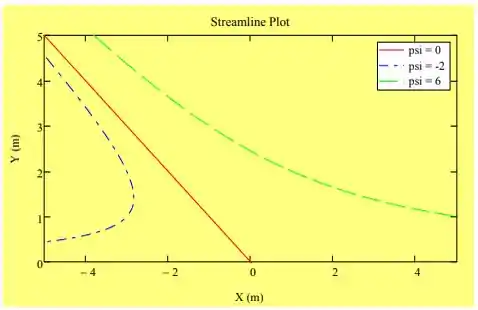
5.80 Considere o campo de escoamento representado pela função de corrente ψ = A x y + A y 2 , em que A = 1   s - 1 . Mostre que este campo de velocidade representa um possível escoamento incompressível. Avalie a rotação do escoamento. Trace algumas linhas de corrente no semiplano superior.

Passo 1

A partir da definição de função de corrente, temos:

u = ∂ ψ ∂ y

u = A x + 2 A y

v = - ∂ ψ ∂ x

v = - A y

Passo 2

Para saber se este campo de velocidade representa um possível escoamento incompressível, vamos começar pela equação da continuidade:

∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z + ∂ ρ ∂ t = 0

Considerando escoamento compressível, então ρ é constante e pode sair da derivada

e ∂ ρ ∂ t = 0 . Considerando, também, ∂ ρ w ∂ z = 0 .

∂ u ∂ x + ∂ v ∂ y = 0

Como u = A x + 2 A y e v = - A y ,

∂ A x + 2 A y ∂ x + ∂ - A y ∂ y = 0

A - A = 0

0 = 0

Como satisfaz a equação, então é um possível escoamento incompressível.

Passo 3

Da definição de rotação:

ω → = 1 2 ∇ × V →

Como:

∇ = i ^ ∂ / ∂ x + j ^ ∂ / ∂ y + k ^ ∂ / ∂ z

E V → = A x + 2 A y i ^ + - A y j ^ ,

ω → = 1 2 i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z A x + 2 A y - A y 0

ω → = 1 2 - 2 A k ^

ω → = - A k ^

Passo 4

Cnsiderando ψ constante, para acharmos a equação para plotar

ψ = A x y + A y 2

x = ψ - A y 2 A y

Resposta

ω → = - A k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14. Um campo de escoamento é simulado por um programa de Dinâmica dos Fluidos Computacional que usa a pressão modificada em seus cálculos. Na Figura P10-14 está um perfil da pressão modificada ao long
11. Considere o escoamento Poiseuille planar do Problema 10-10. Discuta como a pressão modificada varia com a distancia x a jusante. Em outras palavras, a pressão modificada aumenta, permanece a mesma
13. Escreva as três componentes da equação de Navier-Stokes em coordenadas cartesianas em termos da pressão modificada. Insira a definição de pressão modificada e mostre que as componentes x, y e z sã
8. Qual é o parâmetro adimensional na equação de Navier-Stokes na forma admensional que é eliminado pelo uso da pressão modificada em lugar da pressão verdadeira? Explique.
15. No exemplo 9-18 resolvemos a equação de Navier-Stokes para escoamento laminar permanente, completamente desenvolvido em um tubo redondo (escoamento de Poiseuille), desprezando a influencia da grav