Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 48
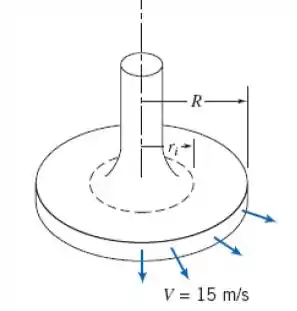
5.48 Considere o escoamento de ar de baixa velocidade entre dois discos paralelos, conforme mostrado. Suponha que o escoamento é incompressível e não viscoso e que a velocidade é puramente radial e uniforme em qualquer seção. A velocidade do escoamento é em . Simplifique a equação da continuidade para uma forma aplicável a este campo de escoamento. Mostre que uma expressão geral para o campo de velocidade é para . Calcule a aceleração de uma partícula fluida em e .
Passo 1
Vamos começar usando a equação da continuidade para coordenadas cinlíndricas:
Vamos considerar regime permanente e, com isso,
Como a velocidade só tem componente em ,
Simplificando, ficamos com:
Se o escoamente é incompressível, então o é constante e pode sair da derivada,
Dividindo por dos dois lados,
Integrando em r,
Onde C é constante.
Como em , , então:
Achamos a constante, então:
O campo fica:
Como queríamos demonstrar.
Passo 2
Como o problema é unidimensional em r e considerando estado estacionário, então a aceleração só vai ter componente x:
Como ,
Passo 3
Para
Para
(Ps.: Como ele não deu o valor de , então vou deixar tudo com letras, ta bom? Então ta bem.)