A componente da velocidade em um campo de escoamento bidimensional, incompressível, é dada por , as coordenadas são medidas em metros e . Não há componente ou variação de velocidade na direção . Calcule a aceleração de uma partícula fluida nos pontos . Estime o raio de curvatura da linha de corrente que passa por este ponto. Trace um gráfico da linha de corrente e mostre os vetores velocidade e aceleração. (Considere a forma mais simples da componente da velocidade em .)

Agora, para encontrar a aceleração de uma partícula desse escoamento, temos:

Então, substituindo o vetor velocidade encontrado no passo 1, temos:

Agora, calculando a velocidade e a aceleração no ponto de interesse (2;1), temos:

Agora, para encontrar o raio de curvatura da linha de corrente, precisamos do valor da aceleração normal e do módulo da velocidade. Então, o vetor normal unitário ao escoamento será:

Então, precisamos também do vetor unitário tangencial, que será dado por:

Então, o vetor normal será:

Então, agora, sabemos que a aceleração normal pode ser escrita como:

E, como sabemos que a componente normal da aceleração é dada por:

Conseguimos encontrar o raio de curvatura substituindo os valores conhecidos:

Agora, para desenhar a linha de corrente, precisamos da sua equação, então, para isso sabemos que a inclinação da linha de corrente é dada por:

Substituindo os valores de e , temos:

Então, integrando essa expressão, temos:

Pela propriedade dos logarítmos, podemos escrever:

Aplicando a exponencial dos dois lados para remover o logarítmo, temos:

Então, para o ponto (2,1), a constante será:

E a equação da linha de corrente será:

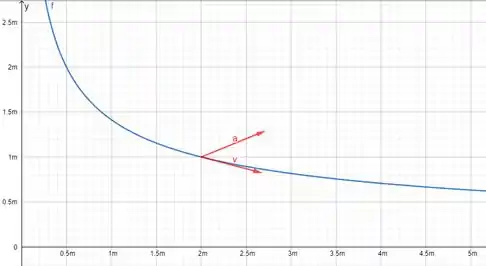
Plotando essa curva, temos: