Calcule as nove componentes do tensor de tensão viscosa em coordenadas cilíndricas (veja o Capítulo 9) para o campo de velocidade do Problema 10-95. Discuta.
Passo 1
O exercício quer que a gente calcule as tensões de cisalhamento (chamadas de tensões viscosas pelo enunciado) presentes no escoamento do problema 10-95. Esse escoamento é mostrado na figura abaixo.
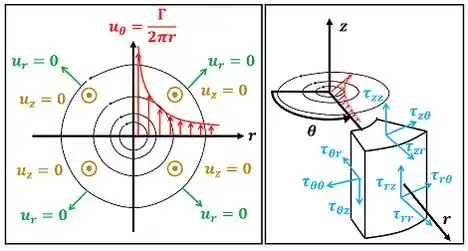
é a velocidade do fluido na direção , é a velocidade do fluido na direção e é a velocidade do fluido na direção . As tensões são as tensões de cisalhamento (tensões viscosas) que queremos descobrir. é a intensidade do vórtice.
No próximo passo nós veremos como podemos utilizar as velocidades dadas par calcular .
Passo 2
Para calcular a partir das velocidades , e , vamos usar a equação 9-63 do livro.
Temos que calcular todas essas derivadas?
Calma! No próximo passo vamos fazer algumas observações que vão simplificar bastante as contas.
Passo 3
Antes de usar essa equação, precisamos fazer uma observação. Como as velocidades não variam com a direção nem com a direção as taxas de variação das velocidades em relação a também chamada de derivada parcial em relação a e em relação a também chamada de derivada parcial em relação a valem zero! Além disso, tanto quanto também valem zero!
Substituindo a fórmula de nas expressões acima, achamos:
Pronto! Encontramos as tensões que queríamos!