Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 97
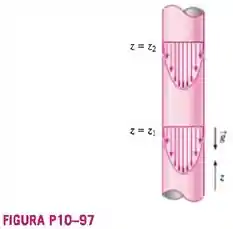
A água desce por um tubo vertical apenas por gravidade. O escoamento entre as posições verticais e é totalmente desenvolvido e os perfis de velocidade nessas duas posições estão representados na Figura P10-97. Como não há gradiente de pressão forçada, a pressão é constante em todos os pontos no escoamento (). Calcule a pressão modificada nas posições e . Desenhe perfis de pressão modificada nas posições e . Discuta.
Passo 1
O problema quer saber quanto vale a pressão modificada em dois planos: um plano que se encontra em e é perpendicular ao escoamento e outro plano que se encontra em que também é perpendicular ao escoamento. A figura abaixo mostra o que a questão quer e ar informações que ela nos oferece.
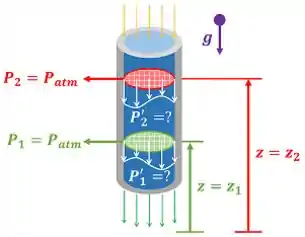
é a pressão absoluta nos pontos localizados em , é a pressão absoluta nos pontos localizados em , é a pressão modificada nos pontos localizados em , é a pressão modificada nos pontos localizados em , é a pressão atmosférica e é a aceleração da gravidade.
Na próxima etapa nós vamos descobrir como usar essas informações para achar e .
Passo 2
A definição de pressão modificada está na equação 10-7. Usando essa equação para e , achamos:
onde é a densidade da água que está escoando no tubo.
No entanto, o enunciado diz que a pressão da água em todo escoamento é igual à pressão atmosférica . Substituindo em e , encontramos e .
Passo 3
Como o valor da coordenada é igual para todo o plano localizado em , percebemos que a pressão modificada é igual em todos os pontos desse plano.
O mesmo vale para o plano localizado em . A pressão modificada é constante em todos os pontos desse plano.
A figura abaixo mostra os perfis de pressão modificada e .
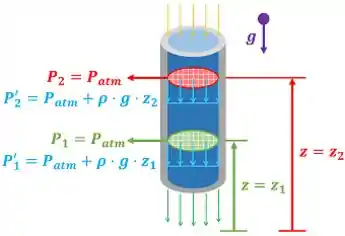
Resposta
