88 – Os dados de desempenho para um modelo muito pequeno (D=8,25 cm) de turbina para água, operando com uma altura de queda disponível de 14,94 m, são os seguintes:

(a) Que tipo de turbina provavelmente é esta? (b) O que há de diferente nesses dados comparados com o gráfico de desempenho adimensional na Figura 11.22d?

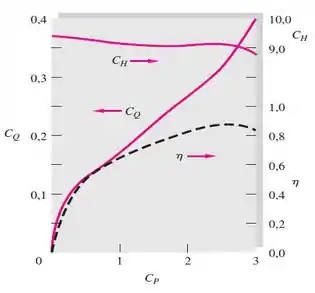
Figura 11.22d – Curvas de desempenho de uma Turbina Francis.

Para n=600 rpm, D=0,7m e Nsp=127.

Suponha que se deseje usar uma turbina geometricamente semelhante para operar onde a altura de queda disponível e a vazão são respectivamente 45,7 m e 192,6 l/s. Calcule o mais eficiente (c) diâmetro da turbina, (d) rotação e (e) potência de eixo.

Precisaremos da potência de eixo de saída, Pe. Esta potência de eixo de saída, lembrando, é a potência que é gerada pela turbina, que vai alimentar o gerador elétrico.

Podemos calcular Pe pela expressão de rendimento da turbina.

O rendimento da turbina é a quantidade de potência que o equipamento gerou, Pe, dividido pela quantidade de potência disponível que a turbina recebeu do fluido, PH, cuja expressão é

Onde,

-η é o rendimento da turbina;

-Pe é a potência de eixo de saída da turbina;

-PH é a potência hidráulica disponível, é a potência que a turbina recebe do fluido;

O rendimento da turbina pode ser entendido também da seguinte forma: é a quantidade percentual de energia que a turbina recebeu do fluido, ou melhor, a quantidade percentual de energia que a turbina removeu do fluido, que escoa por dentro da turbina, para gerar a potência de eixo.

Vamos agora revisar PH

PH como foi dito, é a potência hidráulica disponível, e esta representa a quantidade total de energia disponível que o fluido possui para fornecer à turbina.

Essa variável, lembrando então, é função das propriedades do fluido e da vazão do fluido. A expressão para ela é a seguinte

Onde,

-ρ é a massa especifica (densidade) do fluido (água), que vale 1000 kg/m3 para a água;

-g é constante da gravidade, g=9,81 m/s2;

-Q é a vazão do fluido;

-H é a altura de queda;

Substituindo, a expressão para a eficiência agora é

Isolando Pe

Antes de calcularmos Pe, precisamos dos valores das variáveis da equação acima. Já temos para ρ, g e H, e para Q e η temos os valores da tabela. Para Q e η, você vai pegar os valores correspondentes ao valor de máximo rendimento, ηmáx, ou seja, o maior valor de η e o valor de Q correspondente.

Pela tabela do enunciado

Você pegou esses valores porque é sempre desejável que a turbina opera nas condições ótimas, isto é, na condição de maior rendimento.

Calculando a potência de eixo de saída

Podemos converter as unidades kgm2/s3 para kW, onde kW é equivalente a kJ/s e J é kgm2/s2.

Assim,

Vamos pegar novamente a expressão de Nsp

Precisamos da potência em unidade de hp. Assim, convertendo a potência de eixo de saída da turbina para unidades de hp.

O valor de n, a rotação do rotor, também deve ser o valor para o ponto de máximo rendimento, então pela tabela do enunciado no ponto de máximo rendimento (65%)

Aplicando os valores para o cálculo de Nsp

Agora com esse valor, vamos até a tabela disponível no livro do White, Cap. 11, pág. 799. Com ela podemos ver qual é o tipo de turbina, levando em conta a faixa de valores de Nsp para cada turbina mostrado na tabela, e comparando com o valor de Nsp encontrado.

Para um valor de 65,9, está dentro da faixa de valores para uma turbina do tipo Francis.

A turbina em operação deve ser uma Turbina Francis.

(B)

Para esse item, você só vai precisar identificar há diferença dos dados do enunciado com o gráfico da figura 11.22d. Olhando na descrição da figura 11.22d, você vai ver que o gráfico de desempenho foi construído com um valor especifico de rotação, n, então são dados de desempenho adimensional para uma turbina que opera a uma certa rotação do rotor. Isso é útil para você verificar como o desempenho da turbina varia, para uma certa rotação do rotor, com as mudanças de valores das outras variáveis do projeto.

Já na tabela, para cada valor de vazão e rendimento, temos um valor rotação, n, em rpm. Isso está ao contrário do que foi feito na turbina representada na figura 11.22d. Aqui não podemos verificar o desempenho da turbina com as variações, para um certo valor de rotação, pois a rotação também está variando.

Para as questões (C), (D) e (E), precisamos dos novos valores de D, n e Pe, para H=45,7 m e Q=192,6 L/s. Foi pedido o mais eficiente deles, então temos que achar esses valores para a condições de máximo rendimento da turbina.

O que você pode fazer é usar os coeficientes adimensionais, que são, os coeficientes de vazão, CQ, de altura de queda, CH, e de potência, CP. Na condição de máximo rendimento, os valores de cada coeficiente não se altera, e podemos então usar essa informação para calcular os valores de D, n e Pe mais eficientes, isto é, calcular os novos valores dessas variáveis no ponto de máximo rendimento.

As expressões para o cálculo de cada coeficiente são:

Onde,

-CQ é o coeficiente de vazão;

-Q é a vazão volumétrica do fluido;

-CH é o coeficiente de altura de queda;

-CP é o coeficiente de potência;

-g é constante da gravidade, 9,81 m/s2;

-ρ é a massa especifica (densidade) do fluido (água), que vale 1000 kg/m3 para a água;

-n é a rotação, em rps;

-Pe é a potência de eixo de saída de cada turbina;

-H é a altura de queda.

Primeiramente, vamos calcular cada coeficiente na condição de máximo rendimento. Para isso vamos usar os dados originais.

Calculando CQ*

Calculando CH*

Calculando CP*

Onde, os coeficientes com (*) significam que são os valores dos coeficientes no ponto de máximo rendimento da turbina.

Agora vamos ver como determinar os novos valores de D, n e Pe.

Pelas expressões dos coeficientes, , vemos que não é possível explicitar D ou n sem colocar um em função do outro, então teremos que pegar duas equação para resolver.

Pegando a de CQ primeiro

Isolando n

Pegando agora a expressão de CH*

Substituindo a Eq1 na equação de CH*

Isolando D

Aplicando os valores

Agora vamos voltar na Eq1 e achar n

Aplicando os valores

Em rpm

Para Pe, vamos usar a expressão do coeficiente de potência, CP

Isolando Pe

Aplicando os valores