Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 27
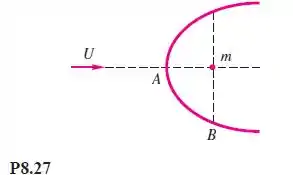
Água a 20ºC escoa ao redor de um semicorpo, como mostra a Figura 8.27. As pressões medidas nos pontos A e B são 160 kPa e 90 kPa, respectivamente, com incertezas de 3 kPa cada. Avalie a velocidade da corrente e sua incerteza.
Passo 1
Bora pra mais uma!
Da equação 8.18 para a superfície de cima, sendo que :
Aplicando Bernoulli:
Daí obtemos:
A incerteza em ( é tão alta quanto 6000Pa, o que implica que a incerteza de U é .
Resposta
A velocidade é 10m/s e com uma incerteza de .
Exercícios de Livros Relacionados
Seja Ψ = 9 + 6 x - 4 y + 7 x y .Verificar se essa função pode ser a função de corrente de um fluido inompressível.Verificar se o escoamento é irrotacionalDeterminar a velocidade no ponto (0,0)
Um campo de escoamento é representado pela função de corrente ψ = x 5 - 10 x 3 y 2 + 5 x y 4 . Determine o campo de velocidade correspondente. Mostre que este campo de escoamento é irrotacional e obte
A função de corrente de um campo de escoamento é ψ = A x 2 y - B y 2 , em que A = 1 m - 1 . s - 1 , B = 1 3m - 1 . s - 1 e as coordenadas são medidas em metros. Encontre uma expressão para o potencial
A função de corrente de um campo de velocidade é ψ = A x 3 + B ( x y 2 + x 2 - y 2 ) , em que ψ , x , y , A e B são todos adimensionais. Encontre a relação entre A e B para esse escoamento. Encontre o
A função de corrente de um campo de velocidade é ψ = A x 3 - B x y 2 , em que A = 1m - 1 . s - 1 e B = 3m - 1 . s - 1 , e as coordenadas são medidas em metros. Encontre a expressão para o potencial de