Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 18

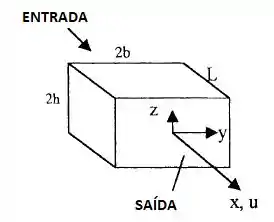
Um fluido incompressível escoa em regime permanente pelo duto retangular da figura a seguir. O perfil de velocidades na saída é dado aproximadamente por

u = u m á x 1 - y 2 b 2 1 - z 2 h 2

(a) Esse perfil satisfaz as condições de contorno corretas para escoamento de fluidos viscosos? (b) Encontre uma expressão analítica para a vazão volumétrica Q na saída. (c) Se a vazão na entrada é de 8,5 m³/min, calcule u m á x em m/s, para b = h = 10   c m .

Passo 1

Vamos lá!!! Vou agora entrar contigo em mais um LERIGOU da mecflu hehe \o/

(a) A primeira coisa pedida você vai enxergar que é algo tranquilo de se verificar, sabe o porquê? Bem, se você se lembrar bem a gente sabe que nas superfícies, nós temos que a velocidade é zero, certo? Então se a gente verificar que em y = ± b e z = ± h a velocidade for zero, teremos que esse perfil satisfaz as condições de contorno corretas.

u = u m á x 1 - - b 2 b 2 1 - z 2 h 2 = 0

u = u m á x 1 - y 2 b 2 1 - ( - h ) 2 h 2 = 0

Note que como temos no perfil um y 2 e um h 2 , o valor dentro dessas variáveis sempre serão positivas, então se para y = - b e z = - h a velocidade já deu zero, COM CERTEZA para seus valores b e h também darão zero, logo o perfil está de acordo com as condições de contorno.

Passo 2

(b) A vazão volumétrica de saída é de boa também, porque uma vez que a gente tem o perfil de velocidade, precisamos apenas integrar na área de escoamento, sacou?

Q = ∬ u d A = ∫ - h + h ∫ - b + b u m á x 1 - y 2 b 2 1 - z 2 h 2 d y d z = u m á x 4 b 3 4 h 3

Q = 16 b h u m á x 9

Passo 3

(c) Agora vem a parte molezinha heheeh, se a gente já tem a expressão analítica da vazão de saída, podemos lembrar do balanço de massa que para um fluido incompressível diz que a vazão de entrada tem que ser igual a vazão de saída.

Q e = Q = 16   x   0,10   x   0,10   x   u m á x 9

Q = 8,5 m 3 m i n x m i n 60 s = 0,14 16   m 3 / s

Resolvendo então temos:

0,14 16 = 16   x   0,1   x   0,1 9 u m á x → u m á x = 8   m / s

Resposta

u m á x = 8   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um funil cônico, com meio ângulo θ = 30 ° , o líquido é drenado através de um pequeno orifício de diâmetro d = 6,25m m no vértice do funil. A velocidade do líquido através do orifício é dada, aprox
Considere um escoamento incompressível e permanente de ar padrão em uma camada limite sobre toda a extensão da superfície porosa mostrada. Considere também que a camada limite na extremidade a jusante
Água escoa de um tanque por um tubo lateral, conforme a figura. A velocidade do escoamento na seção do tubo de descarga é dada por: v = v m á x 1 - r R 2 á Determinar:A taxa de variação com o tempo, n
Na instalação, a vazão de 100 L/s divide-se igualmente nos dois ramais. Qual é o momento em relação ao eixo z devido somente à ação da água? Dados: A 2 = A 3 = 2 ⋅ 10 - 3m 2 ; p 1 = 100P a ; γ = 10 4N
Após a seção de entrada (1) de um conduto de seção quadrada de 0,3 m × 0,3 m , existem duas paredes porosas. A vazão de água na entrada é 300L / s . Pela parede porosa superior (2) há uma vazão de ent