Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 20

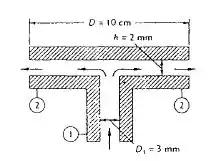
Óleo (d = 0,89) entra na seção 1 da figura abaixo com uma vazão em peso de 250 N/h para lubrificar um mancal de escora. O escoamento permanente de óleo sai radialmente através da folga estreita entre as placas de escora. Calcule (a) a vazão volumétrica na saída em mL/s e (b) a velocidade média na saída em cm/s.

Passo 1

Aqui a gente vai precisar aplicar nosso bendito balanço de massa, beleza?! Então vem comigo, galerinhaaa

Vamos te antemão calcular a densidade do óleo:

ρ ó l e o = d x ρ á g u a = 0,89 979 = 871,3   k g / m ³

Pelo balanço de massa a gente sabe que: Q 2 = Q 1 = Q

Passo 2

(a) Agora vou te ensinar um paranauê dos bons!!! Tá vendo que ele te deu a vazão em N/h? WTF!!!!!!!!

Então, vamos antes lembrar O QUE É newton? F = N = m   a

Então, se a gente fizer N a = m , certo? Ou seja, se a gente pegar esse valor de vazão que ele nos deu e dividirmos pela aceleração, que no caso é a gravidade, vamos obter na unidade que estamos acostumados Kg/h.

Mas não gostamos de trabalhar com unidade hora, então vamos passar pra segundos que é o SI.

Q = 250 N h x   h 3600 s = 0,07   N / s

Dividindo pela gravidade, temos:

Q = 0,07 9,81 = 0,0071   K g / s

Vamos trabalhar com vazão volumétrica?

Q = 0,0071 k g s x 1 ρ ó l e o = 0,0071 k g s 1 871,3 k g m 3 = 8,12   x 10 - 6 m 3 s = 8,12   m L / s

Passo 3

(b) Se eu sei a vazão, com certeza eu sei calcular essa velocidade, certo?

Q 2 = V 2 A 2 = V 2 π D h → V 2 = Q 2 π D h = 8,12   x   10 - 6 π 0,1 0,002 = 1,24 c m s

Resposta

a Q 2 = 8,12   m L / s

b V 2 = 1,24   c m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um escoamento a montante em regime permanente, a massa específica é 1k g / m 3 , a velocidade é 1000m / s , e a área é 0,1m 2 . A jusante, a velocidade é 1500m / s , e a área é 0,25m 2 . Qual é a m
Em sua cozinha, a pia tem 0,6m por 45,7c m e tem 30,5c m de profundidade. Você a está enchendo com água com uma vazão de 252 × 10 - 6m 3 / s . Quanto tempo (em minutos) você leva para encher metade da
Óleo escoa em regime permanente formando uma fina camada em um plano inclinado para baixo. O perfil de velocidade é dado por: Expresse a vazão mássica por unidade de largura em termos de ρ , μ , g , θ
Normas para ventilação de ar em salas de aula especificam uma renovação do ar da sala com uma vazão de pelo menos 8,0L / s de ar fresco por pessoa (estudantes e professor). Um sistema de ventilação pa
Um fluido incompressível escoa em regime permanente por meio de um canal plano divergente. Na seção de entrada, de altura H , o escoamento é uniforme com módulo V 1 . Na saída, de altura 2 H , o perfi