Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 39
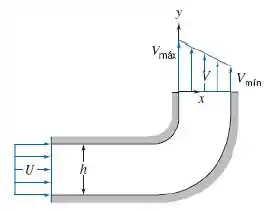
Água entra em um canal bidimensional de largura constante, , com velocidade uniforme, . O canal faz uma curva de que distorce o escoamento de modo a produzir, na saída, o perfil linear de velocidade mostrado com . Avalie , se .
Passo 1
Primeiro nó temos que selecionar s superfície de controle a ser estudada. Aqui nós selecionamos a superfície que está pontilhada.
Passo 2
A segunda coisa a ser feita, é encontrar um perfil de velocidade na seção 2 da superfície de controle. Sabemos que o perfil é linear, pois foi dito no enunciado. Logo, o perfil tem a cara de uma função de primeiro grau:
Temos então que encontrar quem é e quem é . Podemos fazer isso com os dados fornecidos no desenho. Quando o , a velocidade na seção 2 é . Escrevendo isso matematicamente:
Foi dito que , então podemos dizer que:
Agora usamos o outro dado da extremidade, onde, quando o , a velocidade na seção 2 é . Escrevendo isso matematicamente:
Assim temos que o perfil de velocidade será o seguinte:
Passo 3
Agora, podemos aplicar a equação de conservação da massa ao volume de controle:
Em que é o volume de controle, é a densidade do fluido, é o volume do fluido, é a superfície de controle, é o vetor de velocidade, é a área da seção transversal do fluxo.
Podemos fazer as seguintes suposição:
O fluxo é constante e incompressível.
O volume de controle é constante.
Regime é permanente.
Portanto, podemos eliminar a densidade da equação, e como não depende do tempo o primeiro termo da equação também pode ser eliminado.
Assim, a equação da conservação de massa reduz-se a:
Passo 4
Podemos expandir a equação acima para as seções 1 e 2.
Precisamos agora examinar as direções dos vetores. Na seção 1 o vetor de área e velocidade agem em sentidos opostos, logo, o resultado do produto escalar é negativo. Na seção 2 o vetor velocidade a área agem no mesmo sentido, logo, o produto escalar é positivo. Portanto:
Nos foi dado que tem velocidade uniforme igual a . Temos que pode ser escrito como e que pode ser escrito como . Para , nós encontramos o perfil de velocidade. Assim ao substituirmos na equação e integrando de a , temos:
Substituindo por que foi dado no enunciado, vamos encontrar .
Assim, a velocidade mínima é .