Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 25

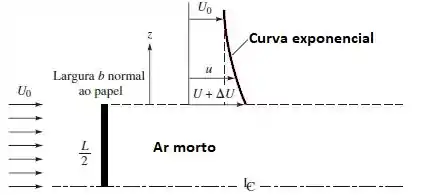
Como será discutido nos capítulos 7 e 8, o escoamento de uma corrente U o sobre uma placa plana normal cria uma grande esteira de baixa velocidade atrás da placa. Um modelo simples é dado pela figura a seguir, com apenas a metade do escoamento mostrado, dada a simetria. O perfil de velocidades atrás da placa é idealizado como sendo de “ar morto” (velocidade próxima de zero) na esteira e com uma velocidade maior que a da corrente, decaindo verticalmente acima da esteira, segundo a variação u ≈ U o + Δ U e - z L , em que L é a altura da placa e z = 0 corresponde ao topo da esteira. Encontre Δ U em função da velocidade da corrente U o .

Passo 1

Essa questão parece sinistra, né? Mas você vai ver que eu estou contigo aí pra gente se livrar de mecflu de uma vez, belê?

Novamente, pelo nosso balanço de massa é dado por Q e = Q s a i para um sistema incompressível e permanente.

Na entrada a gente tem um perfil constante U 0 e na saída temos um perfil dado por U 0 + Δ U e - z L .

Passo 2

Bora agora lembrar do balanço de massa natural que fazemos quase sempre?

Q e = ∫ - L 2 H U 0 d z = U 0 H + L 2

Q s a i = ∫ 0 H U 0 + Δ U e - z L d z  

Q s a i = ∫ 0 H U 0 d z + ∫ 0 H Δ U e - z L d z

Q s a i = U 0 H + Δ U - z e - z L = U 0 H + Δ U L

Passo 3

Portanto ao final a gente vai ter:

U 0 H + L 2 = U 0 H + Δ U L

Δ U = U 0 H + L 2 - U 0 H L = U 0 H + L 2 - H L = U 0 2

Resposta

Δ U = U 0 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motor de foguete opera em regime permanente como mostra a figura abaixo. Os produtos da combustão que escoam através do bocal de descarga aproximam-se de um gás perfeito com peso molecular de 28. P
Água a 20°C escoa em regime permanente através a bifurcação de tubulação mostrada na figura a seguir, entrando na seção 1 com 76 L/min. A velocidade média na seção 2 é de 2,5 m/s. Uma porção do escoam
Em contraste com o foguete de combustível líquido da questão anterior, o foguete com propelente sólido abaixo é autocontido e não possui dutos de entrada. Aplicando uma análise de volume de controle p
Um cilindro sólido de aço de 4,5 cm de diâmetro e 12 cm de comprimento, com massa de 1500g, cai concentricamente por uma cuba vertical de 5 cm de diâmetro cheia de óleo (d = 0,89). Considerando o óleo
Um jato de água bidimensional em regime permanente, com espessura de 4 cm e uma vazão em peso de 1960 N/s, colide com uma barreira em ângulo como mostrado abaixo. A pressão e a velocidade da água são