Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 24

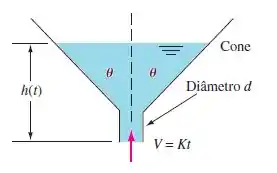
Água entra pelo fundo do cone da figura abaixo com velocidade média uniformemente crescente tal que V = K t . Se d é muito pequeno, obtenha uma fórmula analítica para a elevação do nível d’água h ( t ) com a condição de h 0 = 0 . Considere escoamento incompressível.

Passo 1

Vamos aplicar um volume de controle no nosso cone e fazer uma relação com o balanço de massa, show? Note que pelo balanço temos que:

m ˙ e - m ˙ s = m ˙ a c u m u l a d o = d d t ∫ ρ d v

Não temos saída de fluido, então só temos entrada e o acúmulo, correto?

d d t ∫ ρ d v - m ˙ e = 0

Precisamos calcular então o volume do cone, certo?

v = π 3 r 2 h

Passo 2

Agora vamos calcular o raio do cone!!!

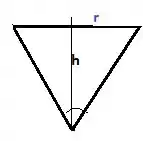
Vamos usar a trigonometria para nos ajudar, beleza?

t a n θ = r h → r = h t a n θ

Agora bora dar uma olhada no nosso balanço de massa?

d d t ∫ ρ d v - m ˙ e = 0 → ρ v = m ˙ e

ρ π 3 r 2 h = m ˙ e

Onde m ˙ e = ρ A V = ρ π d 2 4 K t

Passo 3

Agora meu camarada, é só você literalmente substituir tudo o que encontramos nos passos anteriores dentro do nosso balanço de massa!

ρ π 3 r 2 h = ρ π d 2 4 K t → h t = 3 8 K t 2 d 2 cot 2 ⁡ θ 1 3

Resposta

h t = 3 8 K t 2 d 2 cot 2 ⁡ θ 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma notícia divulgada recentemente na TV sobre o abaixamento do nível do lago Shafer perto de Monticello, Indiana, pelo aumento na descarga através da comporta do lago, as seguintes informações for
Para o funil do Problema 4.55 , determine o diâmetro d requerido se o funil é drenado em t = 1m i n para uma profundidade inicial y 0 = 30c m . Trace o gráfico do diâmetro d requerido para drenar o fu
Um tubo redondo e poroso, com D = 60m m , transporta água. A velocidade de entrada é uniforme com V 1 = 7,0m / s . A água vaza para fora do tubo através das paredes porosas, radialmente e com simetria
O perfil de velocidade para escoamento laminar em uma seção anular é dado por u r = - ∆ p 4 μ L R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r em que Δ p / L = - 10k P a / m é o gradiente de pres
Um tanque retangular, usado para fornecer água em uma experiência de número de Reynolds, tem profundidade de 230m m , largura W = 150m m e comprimento L = 230m m . O número de Reynolds da água do tubo